((本小题满分14分)
已知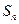 为数列
为数列 的前
的前 项和,且
项和,且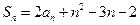 ,
,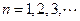 ,
,
(Ⅰ)求证:数列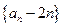 为等比数列;
为等比数列;
(Ⅱ)设 ,求数列
,求数列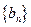 的前
的前 项和
项和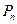 ;
;
(Ⅲ)设 ,数列
,数列 的前
的前 项和为
项和为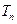 ,求证:
,求证: .
.
((本小题满分13分)
某兴趣小组测量电视塔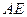 的高度
的高度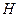 (单位:
(单位: ),如示意图,垂直放
),如示意图,垂直放
置的标杆 的高度
的高度 ,仰角
,仰角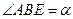 ,
, .
.
(Ⅰ)该小组已经测得一组 、
、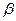 的值,满足
的值,满足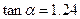 ,
, ,请据此算出
,请据此算出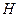
的值;
(Ⅱ)该小组分析若干测得的数据后,认为适当调整
标杆到电视塔的距离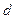 (单位:
(单位: ),使
),使 与
与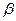
之差较大,可以提高测量精确度。若电视塔的
实际高度为 ,试问
,试问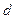 为多少时,
为多少时, 最
最
大?
((本小题满分12分)
已知数列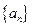 中
中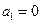 ,
,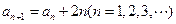 .
.
(Ⅰ)求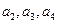 ;
;
(Ⅱ)求数列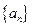 的通项公式;
的通项公式;
(Ⅲ)已知数列 满足
满足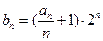
 ,求数列
,求数列 的前
的前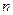 项和.
项和.
((本小题满分12分)
设锐角三角形 的内角
的内角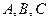 的对边分别为
的对边分别为 ,
,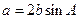 .
.
(Ⅰ)求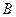 的大小;
的大小;
(Ⅱ)求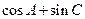 的取值范围.
的取值范围.
(本小题满分12分)
已知函数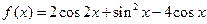 .
.
(Ⅰ)求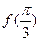 的值;
的值;
(Ⅱ)求 的最大值和最小值.
的最大值和最小值.