
(1) 
(2)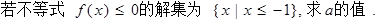
已知抛物线C: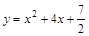 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(1)若C在点M的法线的斜率为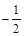 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(2)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
抛物线x2=4y的焦点为F,过点(0,-1)作直线L交抛物线A、B两点,再以AF、BF为邻边作平行四边形FARB,试求动点R的轨迹方程.
已知抛物线y=ax2-1上恒有关于直线x+y=0对称的相异两点,求a的取值范围.
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
(本小题满分12分)
已知函数 ,
, ,且函数
,且函数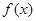 在
在 处取得极值
处取得极值 。
。
(1)求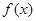 的解析式与单调区间;
的解析式与单调区间;
(2)是否存在实数 ,对任意的
,对任意的 ,都存在
,都存在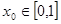 ,使得
,使得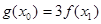 成立?若存在,求出实数
成立?若存在,求出实数 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。