2013年春运期间,长沙火车站在某大学开设了一个服务窗口。假设每一位顾客办理业务所需时间都是整数分钟,对这1000名顾客办理业务所需时间统计结果如下:
| 办理业务所需时间(分钟) |
1 |
2 |
3 |
4 |
5 |
| 人数 |
100 |
400 |
300 |
100 |
100 |
以记录的这1000名顾客办理业务所需时间的频率作为各所需时间发生的概率。
(1)求一位顾客办理业务时间不超过3分钟的概率;
(2)估计顾客办理业务所需时间的平均值。
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
R(x)=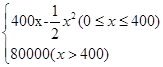 .
.
其中x是仪器的月产量.
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
(1)已知集合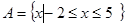 ,
,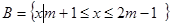 ,若
,若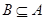 ,求实数m的取值范围?
,求实数m的取值范围?
(2)求值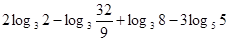
( 12分)函数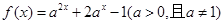
(1)若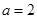 ,求
,求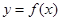 的值域
的值域
(2)若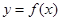 在区间
在区间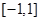 上有最大值14。求
上有最大值14。求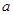 的值;
的值;
(3)在(2)的前题下,若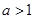 ,作出
,作出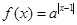 的草图,并通过图象求出函数
的草图,并通过图象求出函数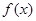 的单调区间
的单调区间
已知函数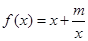 ,且
,且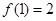
(1)判断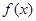 的奇偶性,并证明;
的奇偶性,并证明;
(2)判断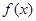 在
在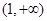 上的单调性,并用定义证明;
上的单调性,并用定义证明;

(3)若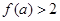 ,求
,求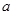 的取值范围。
的取值范围。
(本小题满分14分)
已知函数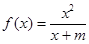 的图像经过点
的图像经过点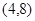 .
.
(1)求该函数的解析式;
(2)数列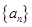 中,若
中,若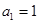 ,
,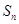 为数列
为数列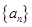 的前
的前 项和,且满足
项和,且满足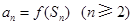 ,
,
证明数列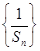 成等差数列,并求数列
成等差数列,并求数列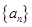 的通项公式;
的通项公式;
(3)另有一新数列 ,若将数列
,若将数列 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
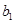 |
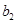 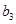 |
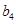 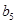 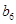 |
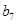 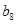 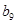 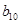 |
记表中的第一列数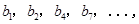 构成的数列即为数列
构成的数列即为数列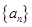 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当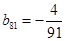 时,求上表中第
时,求上表中第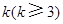 行所有项的和.
行所有项的和.