数列 首项
首项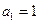 ,前
,前 项和
项和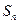 与
与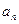 之间满足
之间满足
(1)求证:数列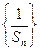 是等差数列
是等差数列
(2)求数列 的通项公式
的通项公式
(3)设存在正数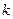 ,使
,使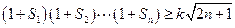 对于一切
对于一切 都成立,求
都成立,求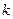 的最大值。
的最大值。
已知圆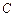 方程为:
方程为: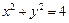 .
.
(1)直线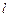 过点
过点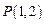 ,且与圆
,且与圆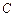 交于
交于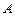 、
、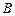 两点,若
两点,若 ,求直线
,求直线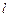 的方程;
的方程;
(2)过圆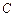 上一动点
上一动点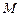 作平行于
作平行于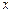 轴的直线
轴的直线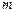 ,设
,设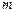 与
与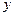 轴的交点为
轴的交点为 ,若向量
,若向量 (
( 为原点),求动点
为原点),求动点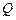 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
( 14分)如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到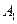 点,且
点,且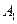 在平面BCD上的射影O恰好在CD上.
在平面BCD上的射影O恰好在CD上.
(Ⅰ)求证: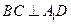 ;
;
(Ⅱ)求证:平面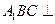 平面
平面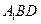 ;
;
(Ⅲ)求三棱锥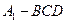 的体积.
的体积. 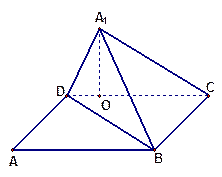
( 12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为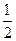 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是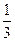 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数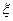 的分布列和数学期望.
的分布列和数学期望.
设函数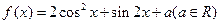 .
.
(1)求函数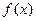 的最小正周期.
的最小正周期.
(2)当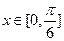 时,
时,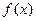 的最大值为2,求
的最大值为2,求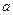 的值,
的值,