设函数f(x)=lnx-ax+ -1.
-1.
(1) 当a=1时, 过原点的直线与函数f(x)的图象相切于点P, 求点P的坐标;
(2) 当0<a< 时, 求函数f(x)的单调区间;
时, 求函数f(x)的单调区间;
(3) 当a= 时, 设函数g(x)=x2-2bx-
时, 设函数g(x)=x2-2bx-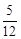 , 若对于
, 若对于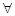 x1∈
x1∈ ,
, 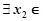 [0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<
[0, 1]使f(x1)≥g(x2)成立, 求实数b的取值范围.(e是自然对数的底, e<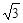 +1).
+1).
已知 (其中
(其中 )的最小正周期为
)的最小正周期为 。
。求
 的单调递增区间;
的单调递增区间;在
 中,
中, 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知 ,求角C。
,求角C。
定义在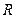 上的函数
上的函数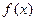 满足
满足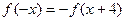 ,当
,当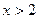 时
时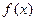 单调递增
单调递增
若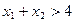 ,且
,且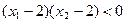 ,判断
,判断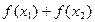 的符号
的符号
(本小题满分12分) 已知函数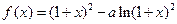 在
在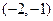 上是增函数,在
上是增函数,在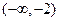 上为减函数.
上为减函数.
(Ⅰ)求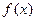 的表达式;
的表达式;
(Ⅱ)若当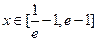 时,不等式
时,不等式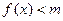 恒成立,求实数
恒成立,求实数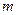 的值;
的值;
(Ⅲ)是否存在实数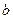 使得关于
使得关于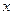 的方程
的方程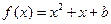 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数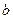 的取值范围.
的取值范围.
(本小题满分12分) 已知双曲线C: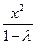
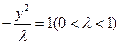 的右焦点为
的右焦点为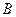 ,过点
,过点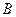 作直线交双曲线C的右支于
作直线交双曲线C的右支于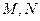 两点,试确定
两点,试确定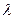 的范围,使以
的范围,使以 为直径的圆过双曲线的中心.
为直径的圆过双曲线的中心.
(本小题满分12分)学校文娱队的每位队员唱
歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中任选2人.设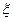 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且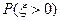 =.
=.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出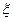 的概率分布列并计算
的概率分布列并计算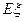 .
.