给出命题p:方程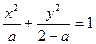 表示焦点在
表示焦点在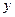 轴上的椭圆;命题q:曲线
轴上的椭圆;命题q:曲线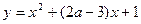 与
与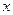 轴交于不同的两点.如果命题“
轴交于不同的两点.如果命题“ ”为真,“
”为真,“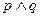 ”为假,求实数
”为假,求实数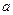 的取值范围
的取值范围
(本小题满分12分)设函数f(x)=m -mx-1.
-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;
(2)对于x∈[1,3],f(x)<0恒成立,求m的取值范围.
(本小题满分12分)
已知抛物线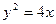 ,焦点为F,顶点为O,点P在抛物线上移动,Q是OP的中点,M是FQ的中点,求点M的轨迹方程.
,焦点为F,顶点为O,点P在抛物线上移动,Q是OP的中点,M是FQ的中点,求点M的轨迹方程.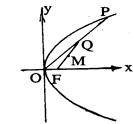
(本小题满分12分)
已知命题 :方程
:方程 有两个不相等的负实根,命题
有两个不相等的负实根,命题 :方程
:方程 无实根;若
无实根;若 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆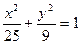 ,直线
,直线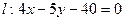 .椭圆上是否存在一点,它到直线
.椭圆上是否存在一点,它到直线 的距离最小?最小距离是多少?
的距离最小?最小距离是多少?