如图,在正三棱柱ABC-A1B1C1中,A1A=AC,D,E,F分别为线段AC,A1A,C1B的中点.
(1)证明:EF∥平面ABC;
(2)证明:C1E⊥平面BDE.
已知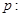 实数
实数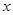 满足
满足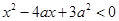 , 其中
, 其中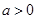 ;
;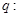 实数
实数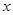 满足
满足 .
.
(1)若 且
且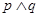 为真, 求实数
为真, 求实数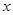 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件, 求实数
的必要不充分条件, 求实数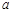 的取值范围.
的取值范围.
(本题13分)已知以椭圆C: 的短轴为直径,以原点为圆心的圆与直线
的短轴为直径,以原点为圆心的圆与直线 相切,且椭圆椭圆C的离心率为
相切,且椭圆椭圆C的离心率为 .
.
(1)求椭圆C的方程;
(2)若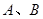 是椭圆C上的两点,且
是椭圆C上的两点,且 轴,
轴, ,连接直线
,连接直线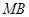 交椭圆C于另一点
交椭圆C于另一点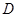 (不同于
(不同于 点),试分析直线
点),试分析直线 与
与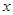 轴是否相交于定点?若是,求出定点坐标;若不是,请加以证明.
轴是否相交于定点?若是,求出定点坐标;若不是,请加以证明.
(本题13分)某市现行出租车收费标准如下:不考虑其他因素下,每次运行起步价为(包括燃油附加费在内)4里内5元(不含4里),满4里后的续程运行价为每里跳表计费1元。
(1)若某乘客坐出租车行驶了 (
( )里,他应付给司机的费用(元)记作
)里,他应付给司机的费用(元)记作 ,求
,求 (
( )的表达式.
)的表达式.
(2)令 ,构造函数
,构造函数 ,
, ,若对任意
,若对任意 ,都有
,都有 恒成立,试求
恒成立,试求 的取值范围.
的取值范围.
(本题12分)如图,在横放得四棱锥E-ABCD中,底面ABCD是正方形,∠DAE=90°,且△ABE是等腰直角三角形,其中∠BAE=90°,连接AC、BD交于点O.
(1)求证:BD⊥平面AEC;
(2)若二面角A-BD-E的大小为60°,且直线EC与平面ABCD所成的角为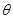 ,求
,求 .
.