已知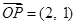 ,
,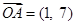 ,
, ,点
,点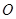 为坐标原点,点
为坐标原点,点 是直线
是直线 上一点,求
上一点,求 的最小值及取得最小值时
的最小值及取得最小值时 的值.
的值.
在
中, 内角
所对的边分别是
. 已知
,
.
(Ⅰ) 求
的值;
(Ⅱ) 求
的值.
某产品的三个质量指标分别为
, 用综合指标
评价该产品的等级. 若
, 则该产品为一等品. 现从一批该产品中, 随机抽取
件产品作为样本, 其质量指标列表如下:
| 产品编号 |
|
|
|
|
|
| 质量指标 | |||||
| 产品编号 |
|
|
|
|
|
| 质量指标 |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件
为 "在取出的
件产品中, 每件产品的综合指标
都等于4", 求事件
发生的概率.
如图,已知曲线
,曲线
,
是平面上一点,若存在过点
的直线与
都有公共点,则称
为"
型点".
(1)在正确证明
的左焦点是"
型点"时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线
与
有公共点,求证
,进而证明原点不是"
型点";
(3)求证:圆
内的点都不是"
型点".
已知函数
,其中常数
;
(1)若
在
上单调递增,求
的取值范围;
(2)令
,将函数
的图像向左平移
个单位,再向上平移1个单位,得到函数
的图像,区间
(
且
)满足:
在
上至少含有30个零点,在所有满足上述条件的
中,求
的最小值.
甲厂以
千克/小时的速度运输生产某种产品(生产条件要求
),每小时可获得利润是
元.
(1)要使生产该产品2小时获得的利润不低于3000元,求
的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大利润.