2014年中国汽车销售量达到2000多万辆,成为世界汽车销售的冠军,各大品牌与国内自主品牌纷纷加大促销力度,争取2015年实现新的突破.某知名品牌的汽车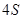 店,对最近
店,对最近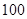 位采用分期付款的购车者进行统计,统计结果如右表所示:已知分
位采用分期付款的购车者进行统计,统计结果如右表所示:已知分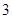 期付款的频率为
期付款的频率为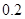 .
.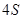 店经销一辆该品牌的汽车,顾客分
店经销一辆该品牌的汽车,顾客分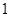 期付款, 其利润为
期付款, 其利润为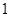 万元;分
万元;分 期或
期或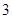 期付款其利润为
期付款其利润为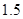 万元;分
万元;分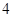 期或
期或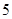 期付款,其利润为
期付款,其利润为 万元.用
万元.用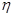 表示经销一辆汽车的利润.
表示经销一辆汽车的利润.
| 付款方式 |
分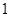 期 期 |
分 期 期 |
分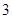 期 期 |
分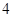 期 期 |
分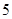 期 期 |
| 频 数 |
40 |
20 |
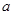 |
10 |
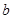 |
(Ⅰ)求上表中的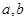 值;
值;
(Ⅱ)若以频率作为概率,求事件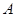 :“购买该品牌汽车的
:“购买该品牌汽车的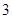 位顾客中,至多有
位顾客中,至多有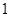 位采用
位采用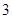 期付款”的概率
期付款”的概率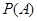 ;
;
(Ⅲ)求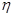 的分布列及数学期望
的分布列及数学期望 .
.
设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足·=0.
(1)求m的值;
(2)求直线PQ的方程.
求过两点A(1,4)、B(3,2),且圆心在直线y=0上的圆的标准方程.并判断点M1(2,3),M2(2,4)与圆的位置关系.
在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合如右图所示.将矩形折叠,使A点落在线段DC上.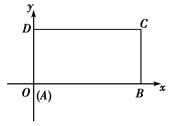
若折痕所在直线的斜率为k,试写出折痕所在直线的方程.
已知△ABC的一个顶点A(-1,-4),∠B、∠C的平分线所在直线的方程分别为l1:y+1=0,l2:x+y+1=0,求边BC所在直线的方程.
已知A(4,-3),B(2,-1)和直线l:4x+3y-2=0,求一点P使|PA|=|PB|,且点P到l的距离等于2.