在平面直角坐标系xOy中,圆C的参数方程为 (
( 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;
(2)设l与圆C相交于A、B两点,求 的值。
的值。
(本小题满分12分)
已知直线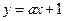 与双曲线
与双曲线 交于A、B两点,
交于A、B两点,
(1)若以AB线段为直径的圆过坐标原点,求实数a的值。
(2)是否存在这样的实数a,使A、B两点关于直线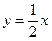 对称?说明理由.
对称?说明理由.
(本小题满分12分)
已知抛物线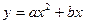 在第一象限内与直线
在第一象限内与直线 相切。此抛物线与x轴所围成的图形的面积记为S。求使S达到最大值的a,b值,并求S的最大值。
相切。此抛物线与x轴所围成的图形的面积记为S。求使S达到最大值的a,b值,并求S的最大值。
如下图,某地有三家工厂,分别位于矩形ABCD 的顶点A、B 及CD的中点P 处,已知AB="20km,CB" ="10km" ,为了处理三家工厂的污水,现要在矩形ABCD 的区域上(含边界),且与A、B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO、BO、OP ,设排污管道的总长度为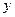 km.
km.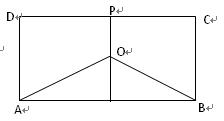
(1)按下列要求写出函数关系式:
①设∠BAO=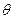 (rad),将
(rad),将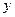 表示成
表示成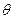 的函数;
的函数;
②设OP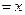 (km) ,将
(km) ,将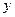 表示成
表示成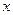 的函数.
的函数.
(2)请选用(1)中的一个函数关系式,确定污水处理厂的位置,使铺设的排污管道总长度最短.
已知函数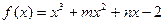 的图像过点
的图像过点 ,且函数
,且函数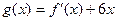 的图象的对称轴为
的图象的对称轴为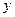 轴
轴
(I)求函数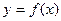 的解析式及它的单调递减区间
的解析式及它的单调递减区间
(II)若函数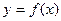 的极小值在区间
的极小值在区间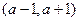 内,求
内,求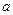 的取值范围
的取值范围
(本题满分10分)已知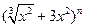 展开式中各项的系数之和比各项的二项式系数之和大992.
展开式中各项的系数之和比各项的二项式系数之和大992.

(Ⅰ)求展开式中二项式系数最大的项;(Ⅱ)求展开式中系数最大的项.