求证:
(本小题满分13分)
高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:
| 分数段 |
(70,90) |
[90,100) |
[100,120) |
[120,150] |
| 人数 |
5 |
a |
15 |
b |
规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.
(Ⅰ)从该班所有学生中任选一名,求其成绩及格的概率;
(Ⅱ)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率;
(Ⅲ)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生的概率.
(本小题满分13分)
已知函数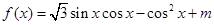
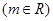 的图象过点
的图象过点 .
.
(Ⅰ)求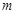 的值;
的值;
(Ⅱ)在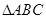 中,角
中,角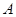 ,
, ,
,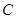 的对边分别是
的对边分别是 ,
,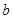 ,
,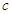 ,若
,若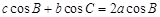 求
求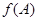 的取值范围.
的取值范围.
数列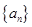 是等差数列,
是等差数列,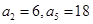 ;数列
;数列 的前n项和是
的前n项和是 ,且
,且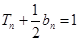 .
.
(1) 求数列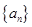 的通项公式; (2) 求证:数列
的通项公式; (2) 求证:数列 是等比数列;
是等比数列;
(3) 记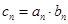 ,求
,求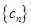 的前n项和
的前n项和
设函数 .
.
(1)求函数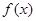 的最小正周期;(2)求函数
的最小正周期;(2)求函数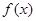 的单调増区间;
的单调増区间;
(3)当 时,求函数
时,求函数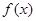 的最大值及取得最大值时的
的最大值及取得最大值时的 的值。
的值。
已知. ,
, 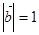
(1)若 的夹角
的夹角 为45°,求
为45°,求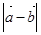
(2)若
 ,求
,求 的夹角
的夹角 .
.