(1)从1,2,3,4,5五个数中依次取2个数,求这两个数的差的绝对值等于1的概率;
(2)△ABC中,∠B=60°,∠C=45°,高AD= ,在BC边上任取一点M,求
,在BC边上任取一点M,求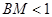 的概率.
的概率.
甲乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码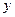 ,设随机变量
,设随机变量
(1)求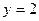 的概率;
的概率;
(2)求随机变量X的分布列及数学期望。
(本小题满分12分)
在 ,角A,B,C的对边分别为
,角A,B,C的对边分别为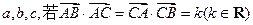 。
。
(1)判断 的形状;
的形状;
(2)若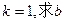 的值。
的值。
(满分12分)已知 为偶函数,曲线
为偶函数,曲线 过点
过点 ,且
,且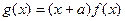 .
.
(Ⅰ)若曲线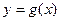 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围
的取值范围
(Ⅱ)若当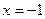 时函数
时函数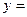
 取得极大值,且方程
取得极大值,且方程 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
(满分12分)函数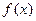 的定义域为
的定义域为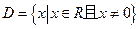 ,且满足对于任意的实数
,且满足对于任意的实数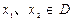 ,有
,有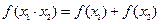 .
.
(Ⅰ)求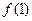 的值; (Ⅱ)判断
的值; (Ⅱ)判断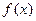 的奇偶性并证明;
的奇偶性并证明;
(I II)若
II)若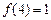 ,且
,且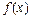 在
在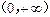 上是增函数,解关于
上是增函数,解关于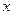 的不等式
的不等式 .
.
(满分12分) 已知函数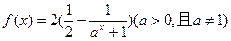 .
.
(Ⅰ)求函数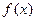 的反函数解析式;
的反函数解析式;
(Ⅱ)判断函数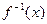 的奇偶性;
的奇偶性;
(III)当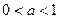 时,
时, 解不定式
解不定式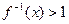 .
.