在研究色盲与性别的关系调查中，调查了男性480人，其中有38-优题课

题文

在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520名女性中有6人患色盲．
(1)根据以上数据建立一个2×2列联表；

(2)若认为“性别与患色盲有关系”，则出错的概率会是多少？
随机变量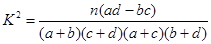
附临界值参考表：

P(K²≥x₀)	0.10	0.05	0.025	0.10	0.005	0.001
x₀	2.706	3.841	5.024	6.635	7.879	10.828

科目数学题型解答题难度容易

相关试题

（本小题满分12分）已知函数．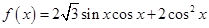
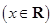（Ⅰ）求函数的最小正周期及在区间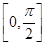上的最大值和最小值；
（Ⅱ）将函数图像向左平移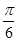个单位，再向上平移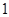个单位，得到函数图像，求的对称轴方程和对称中心坐标．

（本小题满分10分）选修4-5：不等式选讲
已知正实数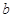，满足：．
（Ⅰ）求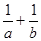的最小值；
（Ⅱ）设函数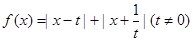，对于（Ⅰ）中求得的，是否存在实数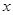，使得成立，若存在，求出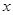的取值范围，若不存在，说明理由．存在使成立

（本小题满分10分）选修4-4：坐标系与参数方程
已知点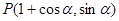，，点在曲线：上．
（Ⅰ）求点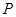的轨迹方程和曲线的直角坐标方程；
（Ⅱ）求的最小值．

（本小题满分10分）选修4-1：几何证明选讲
如图,是圆的直径，是半径的中点，是延长线上一点，且，直线与圆相交于点、（不与、重合），与圆相切于点，连结，，．

（Ⅰ）求证：；
（Ⅱ）若，求．

（本小题满分12分）已知函数，．
（Ⅰ）若，且存在单调递减区间，求的取值范围；
（Ⅱ）设函数的图象与函数的图象交于点、，过线段的中点作轴的垂线分别交、于点、，是否存在点，使在点处的切线与在点处的切线平行？如果存在，求出点的横坐标，如果不存在，说明理由．