对于区间 (或
(或 、
、 、
、 ),我们定义
),我们定义 为该区间的长度,特别地,
为该区间的长度,特别地, 和
和 的区间长度为正无穷大.
的区间长度为正无穷大.
(1)关于 的不等式
的不等式 的解集的区间长度不小于4,求实数
的解集的区间长度不小于4,求实数 的取值范围;
的取值范围;
(2)关于 的不等式
的不等式 恰好有3个整数解,求实数
恰好有3个整数解,求实数 的取值范围.
的取值范围.
(本题8分)
已知直线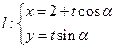 (
(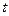 为参数),圆
为参数),圆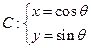 (
(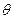 为参数).
为参数).
(Ⅰ)当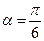 时,试判断直线
时,试判断直线 与圆
与圆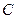 的位置关系;
的位置关系;
(Ⅱ)若直线 与圆
与圆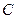 截得的弦长为1,求直线
截得的弦长为1,求直线 的普通方程.
的普通方程.
当实数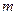 取何值时,复数
取何值时,复数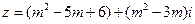
(Ⅰ)是纯虚数;
(Ⅱ)在复平面内表示的点位于直线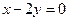 上.
上.
(本小题满分10分)
设 ,函数
,函数 .
.
(Ⅰ) 若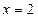 是函数
是函数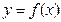 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)求函数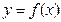 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)若函数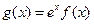 在
在 上是单调递减函数,求实数
上是单调递减函数,求实数 的取值范围.
的取值范围.
(本小题满分10分)
已知数列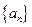 的前
的前 项和为
项和为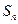 ,
, ,满足
,满足 .
.
(Ⅰ) 计算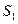 ,
,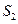 ,
,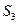 ,
,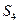 ;
;
(Ⅱ)求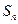 的通项公式.
的通项公式.
(本小题满分10分)
摆地摊的某摊主拿了 个白的,
个白的, 个黑的围棋子放在一个口袋里,并规定凡愿意摸彩者每人交一元钱作手续费,然后一次从口袋摸出
个黑的围棋子放在一个口袋里,并规定凡愿意摸彩者每人交一元钱作手续费,然后一次从口袋摸出 个棋子,中彩情况如下:
个棋子,中彩情况如下:
| 摸棋子 |
 个白棋子 个白棋子 |
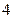 个白棋子 个白棋子 |
 个白棋子 个白棋子 |
其它 |
| 彩金 |
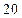 元 元 |
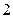 元 元 |
纪念品(价值 角) 角) |
同乐一次(无任何奖品) |
(Ⅰ) 某人交一元钱作手续费,然后一次从口袋摸出 个棋子,求获得彩金
个棋子,求获得彩金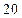 元的概率;
元的概率;
(Ⅱ)某人交一元钱作手续费,然后一次从口袋摸出 个棋子,求无任何奖品的概率;
个棋子,求无任何奖品的概率;
(Ⅲ)按摸彩 次统计,摊主可望净赚约多少钱?(精确到个位)
次统计,摊主可望净赚约多少钱?(精确到个位)