(本小题满分12分)
已知椭圆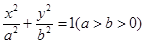 的左右焦点分别为
的左右焦点分别为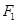 、
、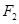 ,由4个点
,由4个点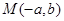 、
、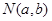 、
、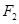 和
和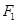 组成一个高为
组成一个高为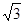 ,面积为
,面积为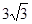 的等腰梯形.
的等腰梯形.
(1)求椭圆的方程;
(2)过点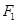 的直线和椭圆交于
的直线和椭圆交于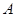 、
、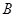 两点,求
两点,求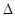
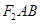 面积的最大值.
面积的最大值.
已知函数 .
.
(Ⅰ)若曲线 在
在 和
和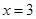 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
已知椭圆 ,椭圆
,椭圆 以
以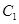 的长轴为短轴,且与
的长轴为短轴,且与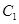 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆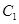 和
和 上,
上,  ,求直线
,求直线 的方程.
的方程.
已知数列 的前
的前 项和
项和 ,数列
,数列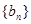 满足
满足
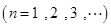 .
.
(Ⅰ)求数列 的通项
的通项 ;(Ⅱ)求数列
;(Ⅱ)求数列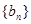 的通项
的通项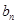 ;
;
(Ⅲ)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
设函数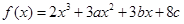 在
在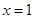 及
及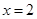 时取得极值.
时取得极值.
(1)求a、b的值;(2)若对于任意的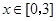 ,都有
,都有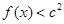 成立,求c的取值范围.
成立,求c的取值范围.
已知椭圆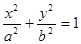 (
(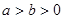 )的右焦点为
)的右焦点为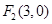 ,离心率为
,离心率为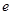 .
.
(Ⅰ)若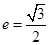 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线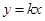 与椭圆相交于
与椭圆相交于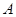 ,
,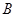 两点,
两点,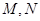 分别为线段
分别为线段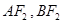 的中点. 若坐标原点
的中点. 若坐标原点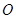 在以
在以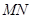 为直径的圆上,且
为直径的圆上,且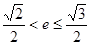 ,求
,求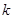 的取值范围.
的取值范围.