如图,在四棱锥 中,底面
中,底面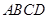 是矩形,侧棱
是矩形,侧棱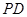 ⊥底面
⊥底面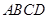 ,
,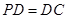 ,
,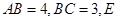 是
是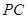 的中点,
的中点,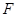 为
为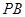 的中点.
的中点.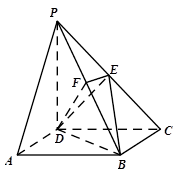
(1)证明: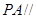 平面
平面
(2)若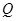 为直线
为直线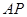 上任意一点,求几何体
上任意一点,求几何体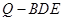 的体积;
的体积;
如图,在四棱锥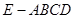 中,底面
中,底面 为正方形,
为正方形,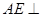 平面
平面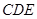 ,已知
,已知 ,
, 为线段
为线段 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求四棱锥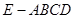 的体积.
的体积.
已知函数 .
.
(1)从区间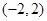 内任取一个实数
内任取一个实数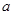 ,设事件
,设事件 ={函数
={函数 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为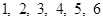 )得到的点数分别为
)得到的点数分别为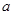 和
和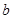 ,记事件
,记事件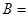 {
{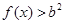 在
在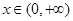 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
已知函数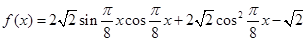 ,
,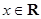 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若函数 图象上的两点
图象上的两点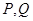 的横坐标依次为
的横坐标依次为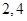 ,
, 为坐标原点,求
为坐标原点,求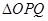 的外接圆的面积.
的外接圆的面积.
已知函数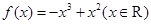 ,
, 满足
满足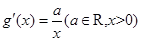 ,且
,且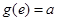 ,
,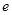 为自然对数的底数.
为自然对数的底数.
(1)已知 ,求
,求 在
在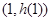 处的切线方程;
处的切线方程;
(2)若存在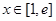 ,使得
,使得
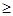
 成立,求
成立,求 的取值范围;
的取值范围;
(3)设函数 ,
,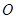 为坐标原点,若对于
为坐标原点,若对于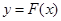 在
在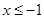 时的图象上的任一点
时的图象上的任一点 ,在曲线
,在曲线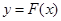
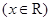 上总存在一点
上总存在一点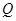 ,使得
,使得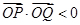 ,且
,且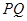 的中点在
的中点在 轴上,求
轴上,求 的取值范围.
的取值范围.
已知动圆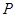 与圆
与圆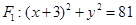 相切,且与圆
相切,且与圆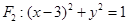 相内切,记圆心
相内切,记圆心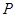 的轨迹为曲线
的轨迹为曲线 ;设
;设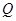 为曲线
为曲线 上的一个不在
上的一个不在 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点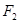 作
作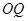 的平行线交曲线
的平行线交曲线 于
于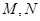 两个不同的点.
两个不同的点.
(1)求曲线 的方程;
的方程;
(2)试探究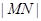 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(3)记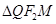 的面积为
的面积为 ,
, 的面积为
的面积为 ,令
,令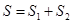 ,求
,求 的最大值.
的最大值.