如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.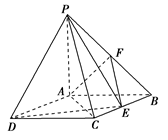
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有 ;
;
(3)当 为何值时,
为何值时,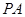 与平面
与平面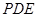 所成角的大小为45°.
所成角的大小为45°.
若数列 满足:存在正整数
满足:存在正整数 ,对于任意正整数
,对于任意正整数 都有
都有 成立,则称数列
成立,则称数列 为周期数列,周期为
为周期数列,周期为 .已知数列
.已知数列 满足
满足 ,
, 则下列结论中错误的是().
则下列结论中错误的是().
A.若 ,则 ,则 可以取3个不同的值; 可以取3个不同的值; |
B.若 ,则数列 ,则数列 是周期为3的数列; 是周期为3的数列; |
C. 且 且 ,存在 ,存在 ,数列 ,数列 周期为 周期为 ; ; |
D. 且 且 ,数列 ,数列 是周期数列. 是周期数列. |
已知函数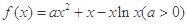 .
.
(1)若函数满足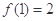 ,且在定义域内
,且在定义域内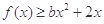 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(2)若函数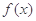 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数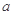 的取值范围;
的取值范围;
(3)当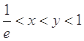 时,试比较
时,试比较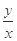 与
与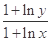 的大小.
的大小.
已知圆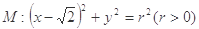 ,若椭圆
,若椭圆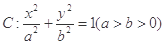 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为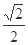 .
.
(1)求椭圆 的方程;
的方程;
(2)若存在直线l:y=kx,使得直线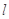 与椭圆
与椭圆 分别交于
分别交于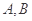 两点,与圆
两点,与圆 分别交于
分别交于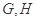 两点,点
两点,点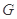 在线段AB上,且
在线段AB上,且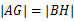 ,求圆M的半径r的取值范围.
,求圆M的半径r的取值范围.
在几何体ABCDE中,AB=AD=BC=CD=2,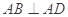 ,且
,且 平面
平面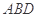 ,平面
,平面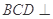 平面
平面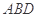 .
.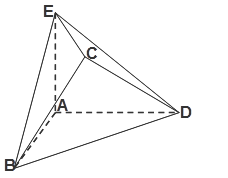
(1)当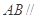 平面
平面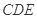 时,求
时,求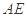 的长;
的长;
(2)当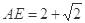 时,求二面角
时,求二面角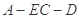 的大小.
的大小.
设函数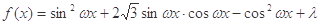 ,
,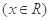 的图象关于直线
的图象关于直线 对称,其中
对称,其中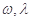 为常数,且
为常数,且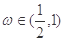 .
.
(1)求函数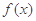 的最小正周期;
的最小正周期;
(2)若 的图象经过点
的图象经过点 ,求函数
,求函数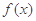 在
在 上的值域.
上的值域.