已知椭圆具有性质:若 是椭圆
是椭圆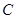 :
: 且
且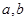 为常数
为常数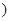 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线 和
和 的斜率都存在,并分别记为
的斜率都存在,并分别记为 ,
, ,那么
,那么 与
与 之积是与点
之积是与点 位置无关的定值
位置无关的定值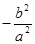 .
.
试对双曲线 且
且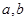 为常数
为常数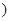 写出类似的性质,并加以证明.
写出类似的性质,并加以证明.
(本小题满分12分)
在 中,角A、B、C的对边分别为a、b、c,面积为S,已知
中,角A、B、C的对边分别为a、b、c,面积为S,已知
(Ⅰ)求证: 成等差数列;
成等差数列;
(Ⅱ)若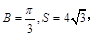 求
求 .
.
(本题满分13分)
设椭圆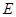 :
: 
 过
过 ,
, 两点,其中
两点,其中 为椭圆的
为椭圆的
离心率, 为坐标原点.
为坐标原点.
(I)求椭圆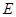 的方程;
的方程;
(II)过椭圆右焦点 的一条直线
的一条直线 与椭圆交于
与椭圆交于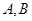 两点,若
两点,若 ,求弦
,求弦 的长.
的长.
(本题满分13分)
已知函数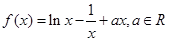 .
.
(I)若函数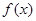 在
在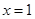 处的切线与
处的切线与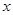 轴平行,求
轴平行,求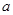 值;
值;
(II)讨论函数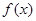 在其定义域内的单调性;
在其定义域内的单调性;
(III)定义:若函数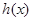 在区间D上任意
在区间D上任意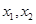 都有
都有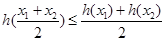 ,则称函数
,则称函数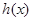 是区间D上的凹函数.设函数
是区间D上的凹函数.设函数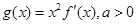 ,其中
,其中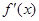 是
是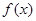 的导函数.根据上述定义,判断函数
的导函数.根据上述定义,判断函数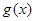 是否为其定义域内的凹函数,并说明理由.
是否为其定义域内的凹函数,并说明理由.
(本题满分13分)
已知正项数列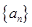 的前
的前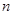 项和为
项和为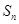 ,且满足
,且满足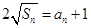 ,
,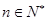 .
.
(I)求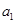 、
、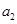 的值,并求数列
的值,并求数列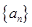 的通项公式;
的通项公式;
(II)设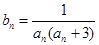 ,数列
,数列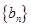 的前
的前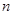 项和为
项和为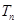 ,证明:
,证明: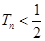 .
.
(本题满分12分)
如图,在四棱锥 中,
中, 为正三角形,
为正三角形, ⊥平面
⊥平面 ,
, ⊥平面
⊥平面 ,
, 为棱
为棱 的中点,
的中点, .
.
(I)求证: ∥平面
∥平面 ;
;
(II)求证:平面 ⊥平面
⊥平面 .
.