操作与探究:
如图,在平面直角坐标系xOy中,已知点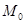 的坐标为(1,0).将线段
的坐标为(1,0).将线段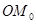 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到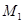 ,使得
,使得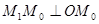 ,得到线段
,得到线段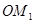 ;又将线段
;又将线段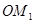 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到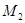 ,使得
,使得 ,得到线段
,得到线段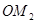 ,如此下去,得到线段
,如此下去,得到线段 ,
,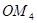 ,…,
,…,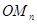 .
.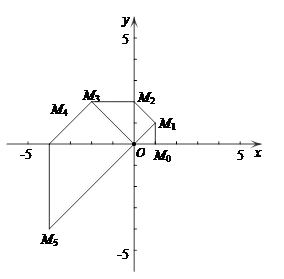
(1)写出点M5的坐标;
(2)求 的周长;
的周长;
(3)我们规定:把点 (
( 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标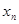 ,纵坐标
,纵坐标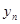 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标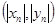 称之为点
称之为点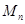 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点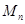 的分布规律,请写出点
的分布规律,请写出点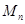 的“绝对坐标”.
的“绝对坐标”.
下表是初三某班女生的体重检查结果:
| 体重(kg) |
34 |
35 |
38 |
40 |
42 |
45 |
50 |
| 人数 |
1 |
2 |
5 |
5 |
4 |
2 |
1 |
根据表中信息,回答下列问题:
(1)该班女生体重的中位数是;
(2)该班女生的平均体重是kg;
(3)根据上表中的数据补全条形统计图.
如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使 .
.
解不等式组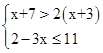 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.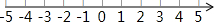
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、
B(0,1)、C(d,2)。
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图
像上。请求出这个反比例函数和此时的直线B′C′的解析式;
(3)在(2)的条件下,直线B′C′交y轴于点G。问是否存在x轴上的点M和反比例函数图像上的点P,
使得四边形PGMC′是平行四边形。如果存在,请求出点M和点P的坐标;如果不存在,请说明理由。
如图,AB是O的直径,AE交O于点E,且与O的切线CD互相垂直,垂足
为D。
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8:
①求O的半径;
②求tan∠BAE的值。