已知：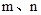
是方程
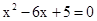的两个实数根，且
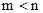，抛物线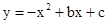
的图像经过点A(
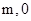)、B(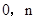
).
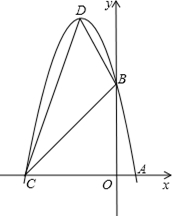
(1)求这个抛物线的解析式；
(2) 设（1）中抛物线与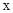
轴的另一交点为C,抛物线的顶点为D，
试求出点C、D的坐标和△BCD的面积；
(3) P是线段OC上的一点，过点P作PH⊥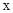轴，与抛物线交于H点，
若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标.
计算：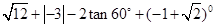
．
如图：已知：E是∠AOB的平分线上的一点，ED⊥OB, EC⊥OA, D、C是垂足，连接CD，求证：（1）∠ECD=∠EDC；(2)OD=OC；（3）OE是CD的中垂线。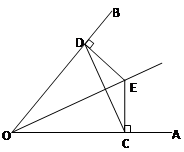 
如图，某船在上午11点30分在A处观测岛B在东偏北30o，该船以10海里/时的速度向东航行到C处，再观测海岛在东偏北60o，且船距海岛40海里．
（1）求船到达C点的时间；
（2）若该船从C点继续向东航行，何时到达B岛正南的D处？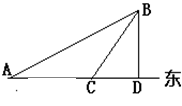
已知，如图：A、E、F、B在一条直线上，AE＝BF，∠C＝∠D，CF∥DE，求证：AC∥BD。
如图，已知点E、C在线段BF上，BE=CF，请在下列四个等式中：①AB＝DE，②∠ACB＝∠F，③∠A＝∠D，④AC＝DF．选出两个作为条件，推出△ABC≌△DEF．并予以证明．（写出一种即可）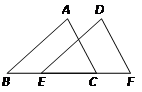
已知：___________，___________．
求证：△ABC≌△DEF
证明：