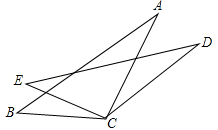
如图，在矩形ABCD中，AB=6，AD=
，点E是AD的三等分点，且AE
DE，过点E作EF∥AB交BC于F，并作射线DC和AB，点P、Q分别是射线DC和射线AB上动点，点P以每秒1个单位的速度向右平移，且始终满足∠PQA=60°，设P点运动的时间为
．
（1）当点Q与点B重合时，求DP的长度；
（2）设AB的中点为N，PQ与线段BE相交于点M，是否存在点P，使△
为等腰三角形？若存在，请直接写出时间的值；若不存在，请说明理由．
（3）设△
与四边形
的重叠部分的面积为S，试求S与的函数关系式和相应的自变量的取值范围．
已知，如图四，△ABC中，BD是AC边上的中线，DB⊥BC于B，且∠ABC=120°，求证：AB=2BC．
如图所示，已知AC∥BD，EA，EB分别平分∠CAB和∠DBA，CD过E点．求证：AB＝AC＋BD．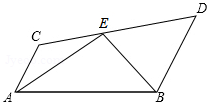
如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=60°，求∠DAC的度数．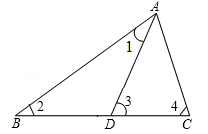
在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-3，0），B（-3，-4），C（-1，-4）．
（1）求△ABC的面积；
（2）在图中作出△ABC关于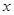
轴对称的图形△DEF，点A、B、C的对称点分别为D、E、F，并写出D、E、F的坐标．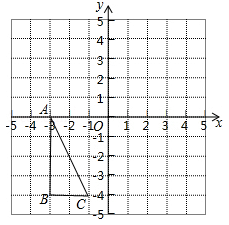
如图，AC=DC，BC=EC，∠ACD = ∠BCE．求证：∠A=∠D．