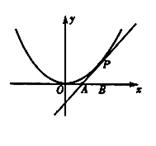
如图,已知直线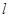 与抛物线
与抛物线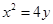 相切于点
相切于点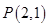 ,且与
,且与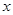 轴交于点
轴交于点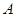 ,
,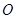 为坐标原点,定点
为坐标原点,定点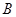 的坐标为
的坐标为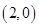 .
. 
(1)若动点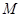 满足
满足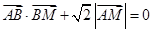 ,求点
,求点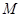 的轨迹
的轨迹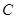 ;
;
(2)若过点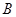 的直线
的直线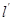 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹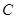 交于不同的两点
交于不同的两点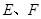 (
(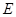 在
在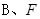 之间),试求△OBE与△OBF面积之比的取值范围.
之间),试求△OBE与△OBF面积之比的取值范围.
想象一下一个人从出生到死亡,在每个生日都测量身高,并作出这些数据的散点图,这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析,下表是一位母亲给儿子做的成长记录:
| 年龄/周岁 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 身高/cm |
91.8 |
97.6 |
104.2 |
110.9 |
115.6 |
122.0 |
128.5 |
| 年龄/周岁 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 身高/cm |
134.2 |
140.8 |
147.6 |
154.2 |
160.9 |
167.5 |
173.0 |
(1)年龄(解释变量)和身高(预报变量)之间具有怎样的相关关系?
(2)如果年龄相差5岁,则身高有多大差异(3~16岁之间)?
(3)如果身高相差20 cm,其年龄相差多少(3~16岁之间)?
(4)计算残差,说明该函数模型是否能够较好地反映年龄与身高的关系,说明理由.
某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如下关系:
| x |
35 |
40 |
45 |
50 |
| y |
56 |
41 |
28 |
11 |
(1)画出散点图,并判断y与x是否具有线性相关关系?
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
在电阻碳含量对于电阻的效应研究中,得到如下表所示的数据:
| 含碳量 (x/%) |
0.10 |
0.30 |
0.40 |
0.55 |
0.70 |
0.80 |
0.95 |
| 20 ℃时电阻 (y/Ω) |
15 |
18 |
19 |
21 |
22.6 |
23.8 |
26 |
(1)求出y与x的相关系数并判断相关性;
(2)求出电阻y关于含碳量x之间的回归直线方程.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
| 分组 |
[29.86,29.90) |
[29.90,29.94) |
[29.94,29.98) |
[29.9830.02), |
[30.02,30.06) |
[30.06,30.10) |
[30.10,30.14) |
| 频数 |
12 |
63 |
86 |
182 |
92 |
61 |
4 |
乙厂:
| 分组 |
[29.86,29.90) |
[29.90,29.94) |
[29.94,29.98) |
[29.9830.02), |
[30.02,30.06) |
[30.06,30.10) |
[30.10,30.14) |
| 频数 |
29 |
71 |
85 |
159 |
76 |
62 |
18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”?
| 甲厂 |
乙厂 |
合计 |
|
| 优质品 |
|||
| 非优质品 |
|||
| 合 计 |
附:
| P(χ2≥x0) |
0.05 |
0.01 |
| x0 |
3.841 |
6.635 |
已知某地每单位面积菜地年平均使用氮肥量x(kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据:
| 年份 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
| x(kg) |
70 |
74 |
80 |
78 |
85 |
92 |
90 |
95 |
| y(t) |
5.1 |
6.0 |
6.8 |
7.8 |
9.0 |
10.2 |
10.0 |
12.0 |
| 年份 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
| x(kg) |
92 |
108 |
115 |
123 |
130 |
138 |
145 |
|
| y(t) |
11.5 |
11.0 |
11.8 |
12.2 |
12.5 |
12.8 |
13.0 |
(1)求x与y之间的相关系数,并检验是否线性相关;
(2)若线性相关,求蔬菜产量y与使用氮肥量x之间的回归直线方程,并估计每单位面积施肥150 kg时,每单位面积蔬菜的年平均产量.
(已知数据: =101,
=101, ≈10.113 3,
≈10.113 3, =161 125,
=161 125, =1 628.55,
=1 628.55,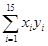 =16 076.8)
=16 076.8)