已知某地每单位面积菜地年平均使用氮肥量x(kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据:
| 年份 |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
| x(kg) |
70 |
74 |
80 |
78 |
85 |
92 |
90 |
95 |
| y(t) |
5.1 |
6.0 |
6.8 |
7.8 |
9.0 |
10.2 |
10.0 |
12.0 |
| |
||||||||
| 年份 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
| x(kg) |
92 |
108 |
115 |
123 |
130 |
138 |
145 |
|
| y(t) |
11.5 |
11.0 |
11.8 |
12.2 |
12.5 |
12.8 |
13.0 |
|
(1)求x与y之间的相关系数,并检验是否线性相关;
(2)若线性相关,求蔬菜产量y与使用氮肥量x之间的回归直线方程,并估计每单位面积施肥150 kg时,每单位面积蔬菜的年平均产量.
(已知数据: =101,
=101, ≈10.113 3,
≈10.113 3, =161 125,
=161 125, =1 628.55,
=1 628.55,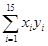 =16 076.8)
=16 076.8)
已知集合 ,集合
,集合
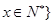 ,集合
,集合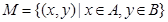
(1)求从集合 中任取一个元素是(3,5)的概率;
中任取一个元素是(3,5)的概率;
(2)从集合 中任取一个元素,求
中任取一个元素,求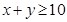 的概率;
的概率;
(3)设 为随机变量,
为随机变量,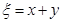 ,写出
,写出 的分布列,并求
的分布列,并求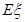 。
。
在 中,
中,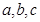 分别是角
分别是角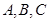 的对边,若
的对边,若 ,
, 。
。
(1)求角 的大小;
的大小;
(2)若 求
求 面积
面积
如图,直角梯形ABMN中,∠NAB=90°,AN∥BM,AB=2,AN= ,BM=
,BM= ,椭圆C以A,B为焦点且过点N.
,椭圆C以A,B为焦点且过点N.
(1)建立适当的坐标系,求椭圆C方程;
(2)若点E满足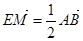 ,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
如图,ABCD是边长为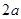 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C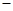 AB
AB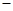 F是直二面角,
F是直二面角,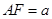 ,G是EF的中点,
,G是EF的中点,
(1)求GB与平面AGC所成角的正弦值.
(2)求二面角B—AC—G的余弦值.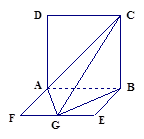
已知 ,讨论方程
,讨论方程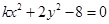 所表示的圆锥曲线类型,并求其焦点坐标
所表示的圆锥曲线类型,并求其焦点坐标