袋中有大小相同的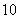 个编号为
个编号为 、
、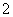 、
、 的球,
的球, 号球有
号球有 个,
个,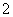 号球有
号球有 个,
个, 号球有
号球有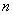 个.从袋中依次摸出
个.从袋中依次摸出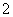 个球,已知在第一次摸出
个球,已知在第一次摸出 号球的前提下,再摸出一个
号球的前提下,再摸出一个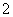 号球的概率是
号球的概率是 .
.
(Ⅰ)求 、
、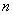 的值;
的值;
(Ⅱ)从袋中任意摸出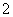 个球,记得到小球的编号数之和为
个球,记得到小球的编号数之和为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
已知函数 (
( 是自然对数的底数)的最小值为
是自然对数的底数)的最小值为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)已知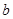
 且
且 ,试解关于
,试解关于 的不等式
的不等式  ;
;
(Ⅲ)已知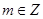 且
且 .若存在实数
.若存在实数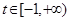 ,使得对任意的
,使得对任意的 ,都有
,都有 ,试求
,试求 的最大值.
的最大值.
已知函数
(Ⅰ)当 时,判断函数
时,判断函数 是否有极值;
是否有极值;
(Ⅱ)若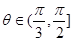 时,
时, 总是区间
总是区间 上的增函数,求实数
上的增函数,求实数 的取值范围.
的取值范围.
某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金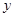 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:① ;②
;②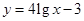 .
.
试分析这两个函数模型是否符合公司要求?
设函数
(Ⅰ)求函数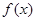 单调递增区间;
单调递增区间;
(Ⅱ)若 时,求
时,求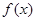 的最小值以及取得最小值时
的最小值以及取得最小值时 的集合.
的集合.
已知函数
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)请用“五点法”作出函数 在区间
在区间 上的简图.
上的简图.