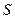某公司拟投资开发某种新能源产品,估计能获得10万元至1000万元的投资收益.为加快开发进程,特制定了产品研制的奖励方案:奖金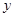 (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
现给出两个奖励模型:① ;②
;②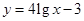 .
.
试分析这两个函数模型是否符合公司要求?
(本小题满分12分)
已知向量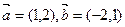 ,
,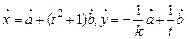 ,k,t为实数.
,k,t为实数.
(Ⅰ)当k=-2时,求使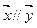 成立的实数t值;
成立的实数t值;
(Ⅱ)若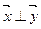 ,求k的取值范围.
,求k的取值范围.
(本小题满分13分)
已知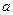 是实数,设函数
是实数,设函数
(1)讨论函数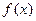 的单调性;
的单调性;
(2)设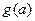 为函数
为函数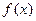 在区间
在区间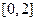 上的最小值
上的最小值
① 写出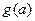 的表达式;
的表达式;
② 求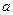 的取值范围,使得
的取值范围,使得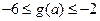
、(本小题满分13分)
已知等差数列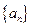 中,
中,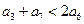 且
且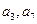 是方程
是方程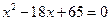 的两根,数列
的两根,数列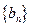 的前项和
的前项和 .
.
(1)求数列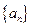 和
和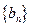 的通项公式;
的通项公式;
(2)记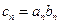 ,求数列
,求数列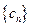 的前
的前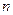 项的和
项的和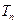 ,并证明
,并证明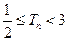
(本小题满分13分)
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元。该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不低于51元
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为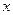 个,零件的实际出厂单价为
个,零件的实际出厂单价为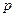 元,写出函数
元,写出函数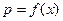 的表达式;
的表达式;
(3)当销售商一次订购多少个时,该厂获得的利润为6000元?(工厂售出一个零件的利润=实际出厂单价—成本)
(本小题满分12分)
已知在△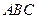 中,角
中,角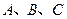 所对的边分别为
所对的边分别为 ,向量
,向量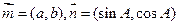
(1)若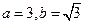 ,且
,且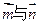 平行,求角
平行,求角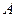 的大小
的大小
(2)若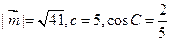 ,求
,求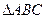 的面积
的面积