如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.
本题满分分 如图,F1,F2是离心率为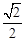 的椭圆C:
的椭圆C: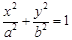 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线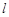 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 :3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.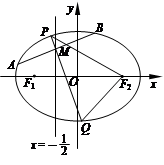
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 求 的取值范围.
的取值范围.
本题满分分 如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形, AF∥DE,AF⊥FE,AF=AD=2 DE=2.
(Ⅰ) 求异面直线EF与BC所成角的大小;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为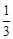 ,求AB的长.
,求AB的长.
本题满分分已知A,B,C,D,E,F是边长为1的正六边形的6个顶点,在顶点取自A,B,C,D,E,F的所有三角形中,随机(等可能)取一个三角形.设随机变量X为取出三角形的面积.
(Ⅰ) 求概率P ( X=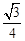 );
);
(Ⅱ) 求数学期望E ( X ).
本题满分分已知函数f (x)=3 sin2 ax+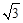 sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
(Ⅰ) 求a的值;
(Ⅱ) 求f (x)的值域.
(本小题满分14分)
设椭圆
 (
( )的两个焦点是
)的两个焦点是 和
和 (
( ),且椭圆
),且椭圆 与圆
与圆 有公共点.
有公共点.
(1)求 的取值范围;
的取值范围;
(2)若椭圆上的点到焦点的最短距离为 ,求椭圆的方程;
,求椭圆的方程;
(3)对(2)中的椭圆 ,直线
,直线
 (
( )与
)与 交于不同的两点
交于不同的两点 、
、 ,若线段
,若线段 的垂直平分线恒过点
的垂直平分线恒过点 ,求实数
,求实数 的取值范围.
的取值范围.