在矩形ABCD中，|AB|=2
，|AD|=2，E、F、G、H分别为矩形四条边的中点，以HF、GE所在直线分别为x，y轴建立直角坐标系(如图所示)．若R、R′分别在线段0F、CF上，且
=
=
.
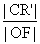(Ⅰ)求证：直线ER与GR′的交点P在椭圆
：
+
=1上；
(Ⅱ)若M、N为椭圆上的两点，且直线GM与直线GN的斜率之积为
，求证：直线MN过定点；并求△GMN面积的最大值．
（本小题满分12分）斜三棱柱
中，侧面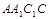
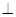底面ABC，侧面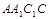是菱形，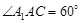
，
，
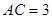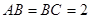，E、F分别是
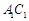，AB的中点．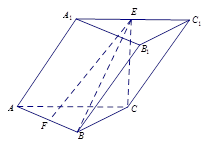
（1）求证：EF∥平面
；
（2）求证：CE⊥面ABC．
（3）求四棱锥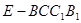
的体积．
（本小题满分12分） 设函数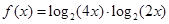
,
,
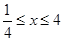（1）若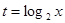
,求
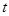取值范围;
（2）求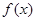
的最值，并给出最值时对应的x的值。
（本小题满分12分）如图，在四棱锥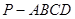
中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E、F分别是AP、AD的中点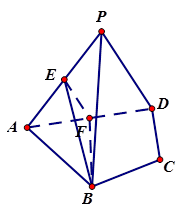
求证：（1）直线EF∥平面PCD；
（2）平面BEF⊥平面PAD
（本小题满分12分）已知两直线l1：x＋my＋6＝0 l2：（m－2）x＋3my＋2m＝0
当m为何值时，l1与l2：
（1）平行；
（2）垂直；
（本小题满分10分） 已知P（3，2），一直线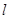
过点P，
①若直线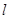在两坐标轴上截距之和为12，求直线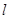的方程；
②若直线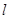与x、y轴正半轴交于A、B两点，当
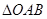面积为12时求直线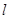的方程．