2012年伦敦奥运会前夕,在海滨城市青岛举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行了7轮比赛,得分的情况如茎叶图所示(单位:分).
| 甲 |
|
乙 |
| 8 |
7 |
9 |
| 5 4 5 4 1 |
8 |
4 4 6 7 4 |
| 1 |
9 |
1 |
(Ⅰ)分别求甲、乙两名运动员比赛成绩的平均分与方差;
(Ⅱ)若从甲运动员的7轮比赛的得分中任选3个不低于80分且不高于90分的得分,求这3个得分与其平均分的差的绝对值都不超过2的概率.
(本小题满分12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度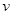 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度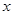 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当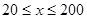 时,车流速度
时,车流速度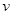 是车流密度
是车流密度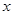 的一次函数.
的一次函数.
(1)当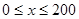 时,求函数
时,求函数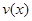 的表达式.
的表达式.
(2)当车流密度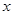 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)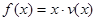 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
(本小题满分12分)设命题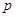 :关于
:关于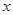 的不等式
的不等式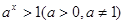 的解集为
的解集为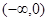 ;命题
;命题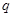 :函数
:函数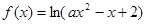 的定义域是
的定义域是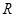 .如果命题“
.如果命题“ ”为真命题,“
”为真命题,“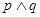 ”为假命题,求
”为假命题,求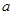 的取值范围.
的取值范围.
(本小题满分12分)已知集合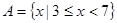 ,
,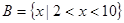 ,
,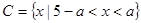 .
.
(1)求 ,
,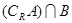 ;
;
(2)若“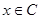 ”是“
”是“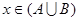 ”的充分条件,求
”的充分条件,求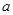 的取值范围.
的取值范围.
(本小题满分12分)已知角 的终边在第二象限,且与单位圆交于点
的终边在第二象限,且与单位圆交于点 .
.
(1)求实数 的值;
的值;
(2)求 的值.
的值.
已知函数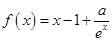 (
(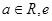 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于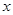 轴,求
轴,求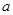 的值;
的值;
(2)讨论函数 的极值情况;
的极值情况;
(3)当 时,若直线
时,若直线 与曲线
与曲线 没有公共点,求k的取值范围.
没有公共点,求k的取值范围.