如图, 为矩形,
为矩形, 为梯形,平面
为梯形,平面
 平面
平面 ,
, ,
, .
.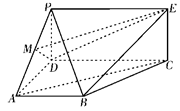
(Ⅰ)若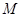 为
为 中点,求证:
中点,求证: ∥平面
∥平面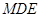 ;
;
(Ⅱ)求平面 与
与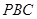 所成锐二面角的大小.
所成锐二面角的大小.
(本小题满分14分)
设函数 是定义在
是定义在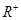 上的减函数,并且满足
上的减函数,并且满足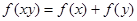 ,
, ,
,
(1)求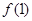 的值, (2)如果
的值, (2)如果 ,求x的取值范围。
,求x的取值范围。
(本小题满分14分)已知点P(2,0),及圆C:x2+y2-6x+4y+4=0.
(1)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(2)设过点P的直线与圆C交于A、B两点,当|AB|=4,求以线段AB为直径的圆的方程.
(本小题满分14分)已知函数 .
.
(1)求函数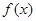 的最小正周期和值域;
的最小正周期和值域;
(2)若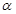 为第二象限角,且
为第二象限角,且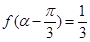 ,求
,求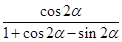 的值.
的值.
(本小题满分14分)已知二次函数 满足
满足 且
且 .
.
(Ⅰ)求 的解析式.
的解析式.
(Ⅱ)在区间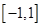 上,
上,  的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的范围.
的范围.
(本小题满分12分)已知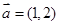 ,
, ,当
,当 为何值时,
为何值时,
(1) 与
与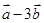 垂直?
垂直?
(2)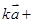
 与
与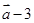
 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?