某超市在节日期间进行有奖促销，凡在该超市购物满300元的顾客，将获得一次摸奖机会，规则如下：
奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就要将奖盒中的球全部摸出才停止．规定摸到红球奖励10元，摸到白球或黄球奖励5元，摸到黑球不奖励．
（Ⅰ）求1名顾客摸球3次停止摸奖的概率；
（Ⅱ）记
为1名顾客摸奖获得的奖金数额，求随机变量的分布列和数学期望．
.
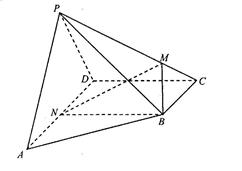
如图，四棱锥P-ABCD的侧面PAD垂直于底面ABCD，∠ADC=∠BCD=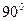
,PA=PD=AD=2BC=2，CD
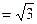,M在棱PC上，N
是AD的中点，二面角M-BN-C为
.
（1）求
的值；
（2）求直线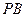
与平面BMN所成角的大小.
某学校餐厅新推出
、
、
、
四款套餐，某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价，对每位同学都进行了问卷调查，然后用分层抽样的方法从调查问卷中抽取20分进行统计，统计结果如下面表格所示：
(1)若同学甲选
择的是
款套餐，求甲的调查问卷被选中的概率；
(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈，求这2人中至少有一人选择的是款套餐的概率。
已知向量
，
．
（I）若
,求
值；
（II）在
中，角
的对边分别是
，且满足
，
求函数
的取值范围．
如图，四棱锥P-ABCD的侧面PAD垂直于底面ABCD，∠ADC=∠BCD=
,PA=PD=AD=2BC=2，CD
,M在棱PC上，N是AD的中点，二面角M-BN-C为
.
（1）求
的值；
（2）求直线
与平面BMN所成角的大小.
（本题满分
12分）
某公司有电子产品
件，合格率为96％，在投放市场之前，决定对该产品进行最后检验，为了减少检验次数，科技人员采用打包的形式进行，即把
件打成一包，对这件产品进行一次性整体检验，如果检测仪器显示绿灯，说明该包产品均为合格品；如果检测仪器显示红灯，说明该包产品至少有一件不合格，须对该包产品一共检测了
次
（1）探求检测这件产品的检测次数
；
（2）如果设
，要使检测次数最少，则每包应放多少件产品？