如图, 是半圆
是半圆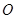 的直径,
的直径, 是半圆
是半圆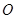 上除
上除 、
、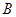 外的一个动点,
外的一个动点,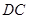 垂直于半圆
垂直于半圆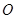 所在的平面,
所在的平面, 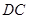 ∥
∥ ,
, ,
,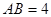 ,
,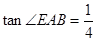 .
.
⑴证明:平面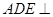 平面
平面 ;
;
⑵当三棱锥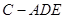 体积最大时,求二面角
体积最大时,求二面角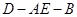 的余弦值.
的余弦值.
(本小题满分16分)
已知函数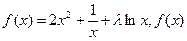 的导数是
的导数是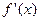 .
.
(1)求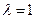 时,
时,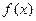 在x=1处的切线方程。
在x=1处的切线方程。
(2)当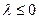 时,求证:对于任意的两个不等的正数
时,求证:对于任意的两个不等的正数 ,有
,有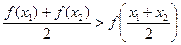 ;
;
(3)对于任意的两个不等的正数 ,若
,若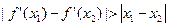 恒成立,求
恒成立,求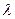 的取值范围.
的取值范围.
(本小题满分16分)
已知数列﹛an﹜中,a2=p(p是不等于0的常数),Sn为数列﹛an﹜的前n项和,若对任意的正整数n都有Sn= .
.
(1)证明:数列﹛an﹜为等差数列;
(2)记bn= +
+ ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;
(3)记cn=Tn-2n,是否存在正整数m,使得当n>m时,恒有cn∈(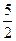 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
.(本小题满分16分)
平面直角坐标系xOy中,已知圆M经过F1(0,-c),F2(0,c),A(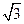 c,0)三点,其中c>0
c,0)三点,其中c>0
(1)求圆M的标准方程(用含c的式子表示);
(2)已知椭圆
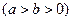 (其中
(其中 )的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
)的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
求椭圆离心率的取值范围;
若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由。
(本小题满分14分)
如图,在半径为R、圆心角为 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.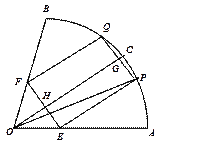
(1)将θ表示为长方形EPQF的面积S(θ)的函数
(2)现用EP和FQ作为母线并焊接起来,将长方形EPQF制成圆柱的侧面,能否从△OEF中直接剪出一个圆面作为圆柱形容器的底面?如果不能,请说明理由;如果能,求出侧面积最大时圆柱形容器的体积.
(本小题满分14分)
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点。
(1)求证:AC⊥DE;
(2)若PB与平面ABCD所成角为450,E是PB上的中点。
求三棱锥P-AED的体积.