(本小题满分16分)
已知函数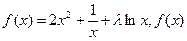 的导数是
的导数是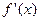 .
.
(1)求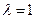 时,
时,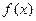 在x=1处的切线方程。
在x=1处的切线方程。
(2)当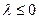 时,求证:对于任意的两个不等的正数
时,求证:对于任意的两个不等的正数 ,有
,有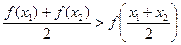 ;
;
(3)对于任意的两个不等的正数 ,若
,若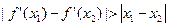 恒成立,求
恒成立,求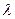 的取值范围.
的取值范围.
在正项等比数列 中,公比
中,公比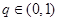 ,
, 且
且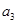 和
和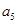 的等比中项是
的等比中项是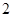 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,判断数列
,判断数列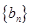 的前
的前 项和
项和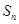 是否存在最大值,若存在,求出使
是否存在最大值,若存在,求出使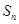 最大时
最大时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在三棱锥 中,
中, 和
和 都是以
都是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 分别是
分别是 的中点.
的中点.
(1)证明:平面 //平面
//平面 ;
;
(2)证明:

 ;
;
(3)若 ,求三棱锥
,求三棱锥 的体积.
的体积.
汽车是碳排放量比较大的行业之一,某地规定,从2014年开始,将对二氧化碳排放量超过 的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:
的轻型汽车进行惩罚性征税。检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位: ).
).
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为 .
.
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过 的概率是多少?
的概率是多少?
(2)求表中 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
已知函数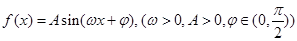 . 的部分图象如图所示,其中点
. 的部分图象如图所示,其中点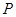 是图象的一个最高点.
是图象的一个最高点.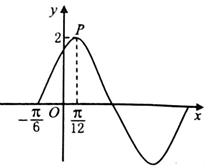
(1)求函数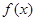 的解析式;
的解析式;
(2)已知 且
且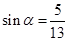 ,求
,求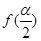 .
.
已知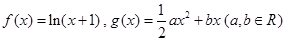 .
.
(1)若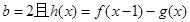 存在单调递减区间,求实数
存在单调递减区间,求实数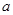 的取值范围;
的取值范围;
(2)若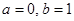 ,求证:当
,求证:当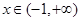 时,
时,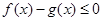 恒成立;
恒成立;
(3)设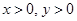 ,证明:
,证明: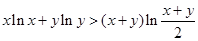 .
.