某高校在2011年的自主招生考试成绩中随机抽取 100名学生的笔试成绩，按成绩分组，得到的频率分布表如下所示．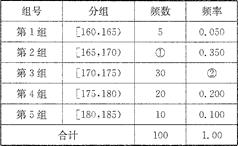
（1）请先求出频率分布表中①，②位置相应的数据，再完成下列频率分布直方图；并确定中位数。（结果保留2位小数）
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试？
（3）在（2）的条件下，学校决定在6名学生中随机抽取2名学生接受考官进行面试，求第4组至少有一名学生被考官A面试的概率？
如图，已知A、B、C是平面α外不共线的三点，并且直线AB、BC、AC分别交α于P、Q、R三点.求证：P、Q、R三点共线.
（本小题满分12分）已知函数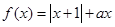
(
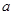∈R).
（1）画出当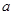=2时的函数
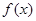的图象；
（2）若函数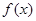在R上具有单调性，求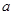的取值范围.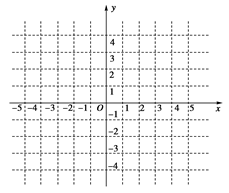
（本小题满分12分）某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品在该售价的基础上每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨
元（为正整数），每个月的销售利润为
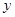元．(14分)
（1）求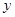与的函数关系式并直接写出自变量的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
证明：函数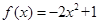
是偶函数，且在
上是减少的。（本小题满分12分）
（本小题满分12分）
已知
，求
的值