在公比为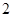 的等比数列
的等比数列 中,
中,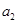 与
与 的等差中项是
的等差中项是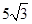 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数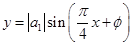 ,
,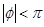 ,的一部分图像如图所示,
,的一部分图像如图所示, ,
, 为图像上的两点,设
为图像上的两点,设 ,其中
,其中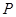 与坐标原点
与坐标原点 重合,
重合,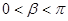 ,求
,求 的值.
的值.
在直角坐标系
中,
的圆心为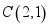 ,半径为1.
,半径为1.
(1)写出 的一个参数方程;
(2)过点 作 的两条切线.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求这两条切线的极坐标方程.
已知抛物线 的焦点为 ,且 与圆 上点的距离的最小值为 .
(1)求 ;
(2)若点 在 上, 是 的两条切线, 是切点,求 面积的最大值.
设函数 ,已知 是函数 的极值点.
(1)求a;
(2)设函数 .证明: .
记 为数列 的前n项和, 为数列 的前n项积,已知 .
(1)证明:数列 是等差数列;
(2)求 的通项公式.
如图,四棱锥 的底面是矩形, 底面 , , 为 的中点,且 .
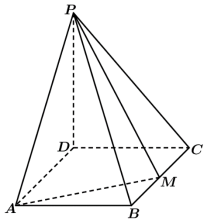
(1)求 ;
(2)求二面角 的正弦值.