如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,
PA=BC=1,PD=AB=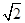 ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.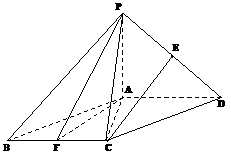
(Ⅰ) 求证:CE∥平面PAF;
(Ⅱ)在线段BC上是否存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°?若存在,试确定G的位置;若不存在,请说明理由.
(本小题满分12分)在 中,已知
中,已知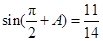 ,
, .
.
(1)求 与
与 的值;
的值;
(2)若角 ,
,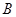 ,
,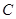 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,求
,求 ,
, 的值.
的值.
(本小题满分14分)已知函数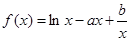 ,对任意的
,对任意的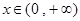 ,满足
,满足 ,其中
,其中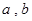 为常数.
为常数.
(1)若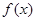 的图像在
的图像在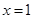 处切线过点
处切线过点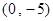 ,求
,求 的值;
的值;
(2)已知 ,求证:
,求证: ;
;
(3)当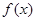 存在三个不同的零点时,求
存在三个不同的零点时,求 的取值范围.
的取值范围.
(本小题满分14分)已知动点 和定点
和定点 ,
, 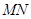 的中点为
的中点为 .若直线
.若直线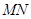 ,
,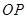 的斜率之积为常数
的斜率之积为常数 (其中
(其中 为原点,
为原点, ),动点
),动点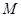 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)曲线 上是否存在两点
上是否存在两点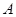 、
、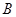 ,使得△
,使得△ 是以
是以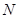 为顶点的等腰直角三角形?若存在,指出这样的三角形共有几个;若不存在,请说明理由.
为顶点的等腰直角三角形?若存在,指出这样的三角形共有几个;若不存在,请说明理由.
(本小题满分14分)设数列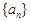 的前
的前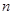 项和为
项和为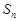 ,满足
,满足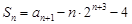 ,
, ,且
,且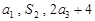 成等比数列.
成等比数列.
(1)求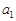 ,
, ,
, 的值;
的值;
(2)令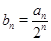 ,求数列
,求数列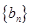 的通项公式;
的通项公式;
(3)证明:对一切正整数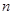 ,有
,有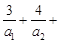
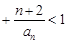 .
.
.(本小题满分14分)如图,已知三棱锥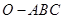 的三条侧棱
的三条侧棱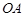 ,
,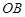 ,
, 两两垂直,△
两两垂直,△ 为等边三角形,
为等边三角形, 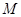 为△
为△ 内部一点,点
内部一点,点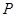 在
在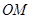 的延长线上,且
的延长线上,且 .
.
(1)证明: ;
;
(2)证明:平面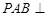 平面
平面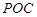 ;
;
(3)若 ,
, ,求二面角
,求二面角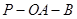 的余弦值.
的余弦值.