(本小题满分12分)在 中,已知
中,已知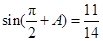 ,
, .
.
(1)求 与
与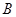 的值;
的值;
(2)若角 ,
,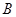 ,
,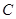 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,求
,求 ,
, 的值.
的值.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是 AB、PC的中点.
(1) 求证:EF∥平面PAD;
(2) 求证:EF⊥CD;
(3) 若∠PDA=45°,求EF与平面ABCD所成的角的大小.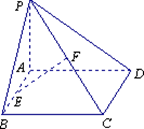
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1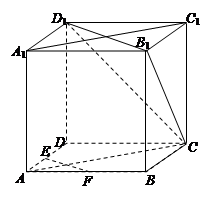
已知函数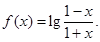
(1)求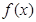 的定义域;(2)证明函数
的定义域;(2)证明函数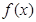 是奇函数。
是奇函数。
如图,在平行四边形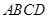 中,边
中,边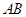 所在直线的方程为
所在直线的方程为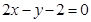 ,点
,点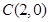 .
.
(1)求直线 的方程;
的方程;
(2)求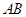 边上的高
边上的高 所在直线的方程.
所在直线的方程.
如图,A、C两岛之间有一片暗礁,一艘小船于某日上午8时从A岛出发,以10海里/小时的速度,沿北偏东75°方向直线航行,下午1时到达B处.然后以同样的速度,沿北偏东15°方向直线航行,下午4时到达C岛.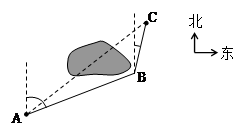
(Ⅰ)求A、C两岛之间的直线距离;
(Ⅱ)求∠BAC的正弦值.