已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是 AB、PC的中点．
(1) 求证：EF∥平面PAD；
(2) 求证：EF⊥CD；
(3) 若∠PDA＝45°，求EF与平面ABCD所成的角的大小．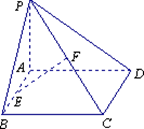
已知函数
的图象过点
.
（1）求实数
的值；
（2）求函数
的最小正周期及最大值.
已知椭圆
的长轴长为
，离心率为
，
分别为其左右焦点．一动圆过点
，且与直线
相切．
（1）(ⅰ)求椭圆
的方程；（ⅱ)求动圆圆心轨迹
的方程；
（2）在曲线上有四个不同的点
，满足
与
共线，
与
共线，且
，求四边形
面积的最小值．
已知函数
(
)
（1）若
在点
处的切线方程为
，求的解析式及单调递减区间；
（2）若在
上存在极值点，求实数
的取值范围．
已知数列
的前
项和
，数列
满足
．
（1）求数列的通项
；
（2）求数列的通项
；
（3）若
，求数列
的前项和
．
如图，已知
为平行四边形，
，
，
，点
在
上，
，
，
与
相交于
．现将四边形
沿折起，使点
在平面
上的射影恰在直线
上．
（1）求证：
平面；
（2）求折后直线
与平面所成角的余弦值．