(本小题满分14分)已知动点 和定点
和定点 ,
, 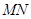 的中点为
的中点为 .若直线
.若直线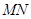 ,
,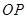 的斜率之积为常数
的斜率之积为常数 (其中
(其中 为原点,
为原点, ),动点
),动点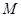 的轨迹为
的轨迹为 .
.
(1)求曲线 的方程;
的方程;
(2)曲线 上是否存在两点
上是否存在两点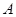 、
、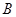 ,使得△
,使得△ 是以
是以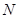 为顶点的等腰直角三角形?若存在,指出这样的三角形共有几个;若不存在,请说明理由.
为顶点的等腰直角三角形?若存在,指出这样的三角形共有几个;若不存在,请说明理由.
( (本小题满分12分)
抛物线 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F A|=2,|FB|=5,
A|=2,|FB|=5,
(1)求直线AB的方程.
(2)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.
((本小题满分12分)
某工厂生产一种 产品,已知该产品的月产量x吨与每吨产品的价格
产品,已知该产品的月产量x吨与每吨产品的价格 (元)之间的关系为
(元)之间的关系为 ,且生产
,且生产 吨的成本为
吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)

((本小题满分12分)
已知函数 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点(1,0)处相切,求a、b
在点(1,0)处相切,求a、b 、c的值.
、c的值.
(本小题满分12分)
求与椭圆 有共同焦点,且过点
有共同焦点,且过点 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。