已知: 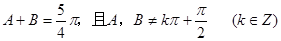
求证: 
已知 都是正数,且
都是正数,且 成等比数列,求证:
成等比数列,求证:
已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为 ,曲线C1,C2相交于A,B两点
,曲线C1,C2相交于A,B两点
(I)把曲线C1,C2的极坐标方程转化为直角坐标方程;
(II)求弦AB的长度.
圆O是 的外接圆,过点C的圆的切线与AB的延长线交于点D,
的外接圆,过点C的圆的切线与AB的延长线交于点D, ,
,
AB=BC=3,求BD以及AC的长.
已知函数 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是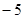 .
.
(1)求实数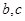 的值;
的值;
(2)求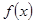 在区间
在区间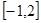 上的最大值;
上的最大值;
(3)对任意给定的正实数 ,曲线
,曲线 上是否存在两点
上是否存在两点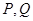 ,使得
,使得 是以
是以 为
为
直角顶点的直角三角形,且此三角形斜边的中点在轴上?请说明理由.
已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为 .
.
(I)求椭圆方程;
(II)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段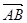 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.