某市蔬菜基地有一批蔬菜若干吨,有三种销售方式,利润如下表
| 销售方式 |
市场直接销售 |
粗加工销售 |
精加工销售 |
| 每吨获利(万 元) |
0.1 |
0.45 |
0.75 |
已知加工能力如下:若蔬菜总量再增加20吨,粗加工刚好10天全部加工完.若蔬菜总量减少20吨,精加工刚好20天全部加工完,且精加工比粗加工每天少加工10吨,又精加工和粗加工不能同时进行,而受季节限制,基地必须要15天(含15天)内全部加工或销售,为此基地特制定了三种方案:①尽可能多的精加工,来不及加工的在市场上直接销售,②全部粗加工,③将一部分精加工,其余蔬菜粗加工,且刚好15天完成.
解答下列问题:(1)求基地这批蔬菜有多少吨?(2)哪种方案获利最多?最多为多少万元?
解分式方程: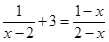
先化简: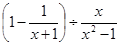 ,再从不等式组
,再从不等式组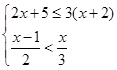 的整数解中选择一个恰当的x值代入并求值.
的整数解中选择一个恰当的x值代入并求值.
如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE//BC交AC于点E,分别过点D、E作DF⊥BC,EG⊥BC,垂足分别为点F、点G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A´、B´、C´处.若A´、B´、C´在矩形DFGE内或者其边上,且互不重合,此时我们称△A´B´C´(即图中阴影部分)为“重叠三角形”.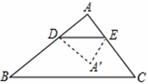
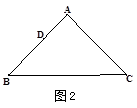
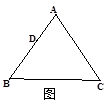
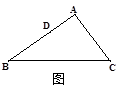

(1)实验操作:当AD=4时,①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,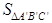 = ;
= ;
②若AB=AC,BC=12,如图3,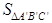 = ;③若∠B=30°,∠C=45°,如图4,
= ;③若∠B=30°,∠C=45°,如图4,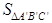 = ;
= ;
(2)实验探究:若△ABC为等边三角形(如图5),设AD的长为m,若重叠三角形A´B´C´存在,试用含m的代数式表示重叠三角形A´B´C´的面积,并写出m的取值范围.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连结DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.当t>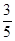 时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
如图,抛物线 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4,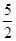 ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.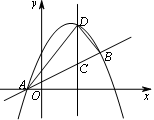
(1)求抛物线的解析式;
(2)设点D的横坐标为m,则用m的代数式表示线段DC的长;
(3)在(2)的条件下,若△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;
(4)当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.