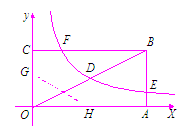
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数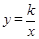 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=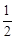 .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
(·湖北孝感)在平面直角坐标系中,抛物线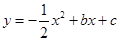 与
与 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 ,直线
,直线 经过
经过 ,
, 两点.
两点.
(1)求抛物线的解析式;
(2)在 上方的抛物线上有一动点
上方的抛物线上有一动点 .
.
①如图1,当点 运动到某位置时,以
运动到某位置时,以 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点 的坐标;
的坐标;
②如图2,过点 ,
, 的直线
的直线 交
交 于点
于点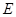 ,若
,若 ,求
,求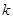 的值.
的值.
(·湖北孝感)如图,四边形 是矩形纸片,
是矩形纸片, .对折矩形纸片
.对折矩形纸片 ,使
,使 与
与 重合,折痕为
重合,折痕为 ;展平后再过点
;展平后再过点 折叠矩形纸片,使点
折叠矩形纸片,使点 落在
落在 上的点
上的点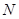 ,折痕
,折痕 与
与 相交于点
相交于点 ;再次展平,连接
;再次展平,连接 ,
, ,延长
,延长 交
交 于点
于点 .
.
有如下结论: ;
;
② ;
;
③ ;
;
④△ 是等边三角形;
是等边三角形;
⑤ 为线段
为线段 上一动点,
上一动点, 是
是 的中点,则
的中点,则 的最小值是
的最小值是 .
.
其中正确结论的序号是 .
(·湖北襄阳,26题)边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.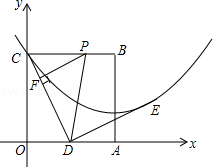
(1)求抛物线的解析式;
(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
(·湖北武汉,24题,分)(本题12分)已知抛物线y=
 +c与x轴交于A(-1,0),B两点,交y轴于点C
+c与x轴交于A(-1,0),B两点,交y轴于点C
(1) 求抛物线的解析式
(2) 点E(m,n)是第二象限内一点,过点E作EF⊥x轴交抛物线于点F,过点F作FG⊥y轴于点G,连接CE、CF,若∠CEF=∠CFG,求n的值并直接写出m的取值范围(利用图1完成你的探究)
(3) 如图2,点P是线段OB上一动点(不包括点O、B),PM⊥x轴交抛物线于点M,∠OBQ=∠OMP,BQ交直线PM于点Q,设点P的横坐标为t,求△PBQ的周长

(·湖北荆门,24题,分)如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.