镇政府想了解对王家村进行"精准扶贫"一年来村民的经济情况,统计员小李用简单随机抽样的方法,在全村130户家庭中随机抽取20户,调查过去一年的收入(单位:万元),从而去估计全村家庭年收入情况.
已知调查得到的数据如下:
1.9,1.3,1.7,1.4,1.6,1.5,2.7,2.1,1.5,0.9,2.6,2.0,2.1,1.0,1.8,2.2,2.4,3.2,1.3,2.8
为了便于计算,小李在原数据的每个数上都减去1.5,得到下面第二组数:
0.4,﹣0.2,0.2,﹣0.1,0.1,0,1.2,0.6,0,﹣0.6,1.1,0.5,0.6,﹣0.5,0.3,0.7,0.9,1.7,﹣0.2,1.3
(1)请你用小李得到的第二组数计算这20户家庭的平均年收入,并估计全村年收入及全村家庭年收入超过1.5万元的百分比;已知某家庭过去一年的收入是1.89万元,请你用调查得到的数据的中位数推测该家庭的收入情况在全村处于什么水平?
(2)已知小李算得第二组数的方差是 S,小王依据第二组数的方差得出原数据的方差为(1.5+ S) 2,你认为小王的结果正确吗?如果不正确,直接写出你认为正确的结果.
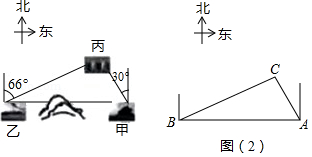
如图,已知甲地在乙地的正东方向,因有大山阻隔,由甲地到乙地需要绕行丙地.已知丙地位于甲地北偏西30°方向,距离甲地460 km,丙地位于乙地北偏东66°方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点 A、 B、 C,可抽象成图(2)所示的三角形,求甲乙两地之间直达高速线路的长 AB(结果用含非特殊角的三角函数和根式表示即可).
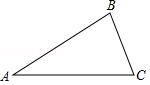
如图,在△ ABC中,内角 A、 B、 C所对的边分别为 a、 b、 c.
(1)若 a=6, b=8, c=12,请直接写出∠ A与∠ B的和与∠ C的大小关系;
(2)求证:△ ABC的内角和等于180°;
(3)若 ,求证:△ ABC是直角三角形.
如图,抛物线 y= ax 2+ bx﹣2( a≠0)与 x轴交于 A(﹣3,0), B(1,0)两点,与 y轴交于点 C,直线 y=﹣ x与该抛物线交于 E, F两点.
(1)求抛物线的解析式.
(2) P是直线 EF下方抛物线上的一个动点,作 PH⊥ EF于点 H,求 PH的最大值.
(3)以点 C为圆心,1为半径作圆,⊙ C上是否存在点 M,使得△ BCM是以 CM为直角边的直角三角形?若存在,直接写出 M点坐标;若不存在,说明理由.

(1)【探究发现】
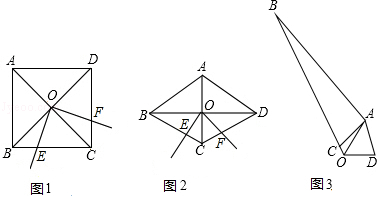
如图1,∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处,∠ EOF=90°,将∠ EOF绕点 O旋转,旋转过程中,∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F(点 F与点 C, D不重合).则 CE, CF, BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的"正方形 ABCD"改为"∠ BCD=120°的菱形 ABCD",其他条件不变,当∠ EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3,∠ BOD=120°, OD= , OB=4, OA平分∠ BOD, AB= ,且 OB>2 OA,点 C是 OB上一点,∠ CAD=60°,求 OC的长.