已知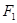 、
、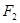 分别为椭圆
分别为椭圆 :
: 的上、下焦点,其中
的上、下焦点,其中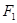 也是抛物线
也是抛物线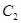 :
:  的焦点,点
的焦点,点 是
是 与
与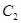 在第二象限的交点,且
在第二象限的交点,且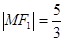 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点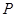 (1,3)和圆
(1,3)和圆 :
: ,过点
,过点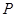 的动直线
的动直线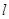 与圆
与圆 相交于不同的两点
相交于不同的两点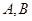 ,在线段
,在线段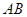 取一点
取一点 ,满足:
,满足: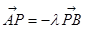 ,
,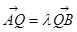 (
( 且
且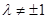 )。
)。
求证:点 总在某定直线上。
总在某定直线上。
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在 ,
, 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为
的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望. 
已知公差不为0的等差数列 的前n项和为
的前n项和为 ,
, ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前n项和.
的前n项和.
已知函数 .
.
(1)求函数 的最大值;
的最大值;
(2)若直线 是函数
是函数 的对称轴,求实数
的对称轴,求实数 的值.
的值.
已知函数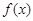 的定义域为
的定义域为 ,且
,且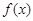 的图象连续不间断. 若函数
的图象连续不间断. 若函数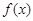 满足:对于给定的
满足:对于给定的 (
( 且
且 ),存在
),存在 ,使得
,使得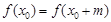 ,则称
,则称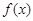 具有性质
具有性质 .
.
(Ⅰ)已知函数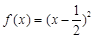 ,
, ,判断
,判断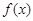 是否具有性质
是否具有性质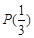 ,并说明理由;
,并说明理由;
(Ⅱ)已知函数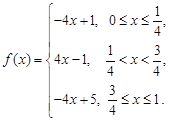 若
若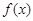 具有性质
具有性质 ,求
,求 的最大值;
的最大值;
(Ⅲ)若函数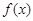 的定义域为
的定义域为 ,且
,且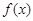 的图象连续不间断,又满足
的图象连续不间断,又满足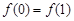 ,
,
求证:对任意 且
且 ,函数
,函数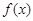 具有性质
具有性质 .
.
已知点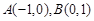 ,点
,点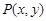 为直线
为直线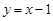 上的一个动点.
上的一个动点.
(Ⅰ)求证: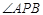 恒为锐角;
恒为锐角;
(Ⅱ)若四边形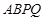 为菱形,求
为菱形,求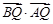 的值.
的值.