数列 中,
中,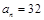 ,
, ,
,
(1)若数列 为公差为11的等差数列,求
为公差为11的等差数列,求
(2)若数列 为以
为以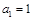 为首项的等比数列,求数列
为首项的等比数列,求数列 的前m项和
的前m项和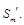
已知函数f(x)=1+sinxcosx.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)若tanx=2,求f(x)的值.
设数列{an}满足当n>1时,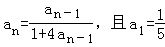 .
.
(1)求证:数列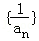 为等差数列;
为等差数列;
(2)试问a1a2是否是数列{an}中的项.如果是,是第几项;如果不是,说明理由.
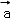 ,
,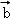 的夹角为120°,|
的夹角为120°,|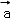 |=1,|
|=1,|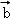 |=3.
|=3.
(1)7;
(2)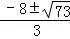 .
.
设函数f(x)=﹣ x(x∈R),其中m>0.
x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)求函数f(x)的单调区间与极值;
(3)已知函数f(x)有三个互不相同的零点0,x1,x2,且x1<x2,若对任意的x∈[x1,x2],f(x)>f(1)恒成立,求m的取值范围.
已知{an}的前n项和Sn,an>0且an2+2an=4Sn+3
(1)求{an}的通项公式;
(2)若bn=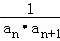 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.