如图,已知正方体 ,
, 分别为各个面的对角线;
分别为各个面的对角线;
(1)求证: ;
;
(2)求异面直线 所成的角.
所成的角.
已知函数 在定义域
在定义域 上为增函数,且满足
上为增函数,且满足
(1)求 的值 (2)解不等式
的值 (2)解不等式
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
(Ⅰ)写出所有可能的数对( ,并计算
,并计算 ,且
,且 的概率;
的概率;
(Ⅱ)求函数 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.
为了调查某厂2000名工人生产某种产品的能力,随机抽查了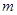 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为 ,
, ,
, ,
, ,
,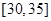 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求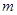 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工人不在同一组的概率是多少?
已知函数f(x)=x2+2ax-3:
(1)如果f(a+1)-f(a)=9,求a的值;(2)问a为何值时,函数的最小值是-4。
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4。现从盒子中随机抽取卡片.
(I)若一次抽取3张卡片,求3张卡片上数字之和大于7的概率;
(II)若第一次抽1张卡片,放回后再抽取1张卡片,求两次抽取中至少一次抽到数字3的概率.