已知函数 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直。
垂直。
(1)求实数 的值;
的值;
(2)若函数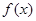 在区间
在区间 上单调递增,求
上单调递增,求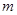 的取值范围.
的取值范围.
(本小题满分12分)(理科做)如图,四棱锥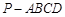 的底面
的底面 是直角梯形,
是直角梯形,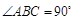 ,
, ,且
,且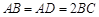 ,顶点
,顶点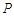 在底面
在底面 内的射影恰好落在
内的射影恰好落在 的中点
的中点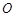 上.
上.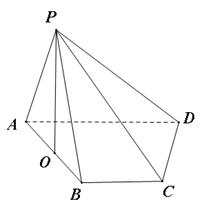
(1)求证: ;
;
(2)若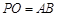 ,求直线
,求直线 与
与 所成角的 余弦值;
所成角的 余弦值;
(3)若平面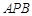 与平面
与平面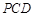 所成的二面角为
所成的二面角为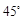 ,求
,求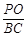 的值.
的值.
(文科做)设函数 .
.
(1)当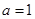 时,试求函数
时,试求函数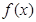 在区间
在区间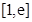 上的最大值;
上的最大值;
(2)当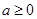 时,试求函数
时,试求函数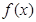 的单调区间.
的单调区间.
(本小题满分12分)甲乙两人各有 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间 ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
(本小题满分12分)已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 交椭圆
交椭圆 于
于 两点,当
两点,当 时求直线
时求直线 的方程
的方程
(本小题满分12分)某市为了解全市居民日常用水量的分布情况,现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如下图表:
| 分组 |
频数 |
频率 |
| [0,1) |
25 |
y |
| [1,2) |
0.19 |
|
| [2,3) |
50 |
x |
| [3,4) |
0.23 |
|
| [4,5) |
0.18 |
|
| [5,6] |
5 |

(Ⅰ)分别求出x,n,y的值;
(Ⅱ)若从样本中月均用水量在[5,6]内的5位居民a,b,c,d,e中任选2人作进一步的调查研究,求居民a被选中的概率.
(本小题满分10分)已知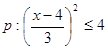 ,
,  若
若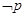 是
是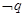 的必要非充分条件,求实数
的必要非充分条件,求实数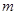 的取值范围.
的取值范围.