一列火车在平直的铁轨上行驶,由于遇到紧急情况,火车以速度 (单位:m/s)紧急刹车至停止。求:
(单位:m/s)紧急刹车至停止。求:
(I)从开始紧急刹车到火车完全停止所经过的时间;
(II)紧急刹车后火车运行的路程。
设函数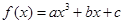
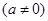 为奇函数,其图象在点
为奇函数,其图象在点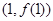 处的切线与直线
处的切线与直线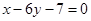 垂直,导函数
垂直,导函数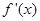 的最小值为
的最小值为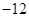 .试求
.试求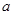 ,
,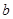 ,
,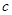 的值。
的值。
(本小题满分14分)
已知函数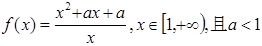
(1)判断 的单调性并证明;
的单调性并证明;
(2)若 满足
满足 ,试确定
,试确定 的取值范围。
的取值范围。
(3)若函数 对任意
对任意 时,
时,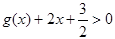 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(本小题满分13分)
已知函数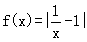
(Ⅰ)判断f(x)在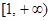 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅱ)若集合A="{y" | y=f(x),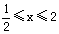 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;
(本小题满分12分)
已知函数
⑴ 若 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。
⑵ 求 在区间
在区间 上的最小值
上的最小值 的表达式。
的表达式。