已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在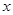 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线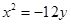 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点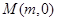 的直线
的直线 与椭圆
与椭圆 相切
相切 ,直线
,直线 与
与 轴交于点
轴交于点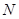 ,当
,当 为何值时
为何值时 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.
移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元. 国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率. 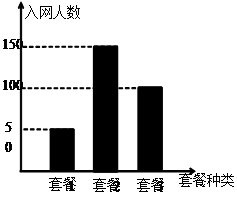
(1)求某人获得优惠金额不低于300元的概率;
(2)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选出两人,求这两人获得相等优惠金额的概率.
已知函数 的图象的两条相邻对称轴之间的距离为
的图象的两条相邻对称轴之间的距离为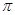 ,
,
(1)求 的值;
的值;
(2)若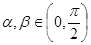 ,
,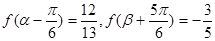 ,求
,求 的值。
的值。
(本小题满分10分)选修4-5:不等式选讲
已知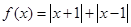 ,不等式
,不等式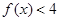 的解集为
的解集为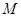 .
.
(1)求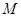 ;
;
(2)当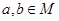 时,证明:
时,证明: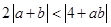 .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线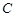 的参数方程为
的参数方程为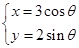 (
(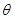 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换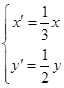 得到曲线
得到曲线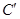 .
.
(1)求曲线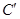 的普通方程;
的普通方程;
(2)若点 在曲线
在曲线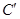 上,点
上,点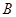
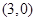 ,当点
,当点 在曲线
在曲线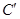 上运动时,求
上运动时,求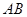 中点
中点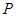 的轨迹方程.
的轨迹方程.
(本小题满分10分)选修4—1,几何证明选讲
如图所示,圆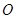 的两弦
的两弦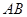 和
和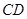 交于点
交于点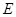 ,
,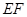 ∥
∥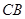 ,
,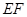 交
交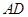 的延长线于点
的延长线于点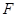 ,
,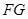 切圆
切圆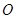 于点
于点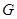 .
.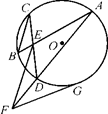
(1)求证:△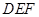 ∽△
∽△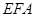 ;
;
(2)如果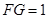 ,求
,求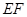 的长.
的长.