已知 是实数,函数
是实数,函数 ,
, 和
和 ,分别是
,分别是 的导函数,若
的导函数,若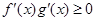 在区间
在区间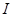 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间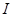 上单调性一致.
上单调性一致.
(Ⅰ)设 ,若函数
,若函数 和
和 在区间
在区间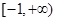 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围;
(Ⅱ)设 且
且 ,若函数
,若函数 和
和 在以
在以 为端点的开区间上单调性一致,求
为端点的开区间上单调性一致,求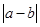 的最大值.
的最大值.
已知函数 在
在 处取得极值.
处取得极值.
(1)求a、b的值;
(2)求过点 且与曲线
且与曲线 相切的切线方程.
相切的切线方程.
用数学归纳法证明 .
.
某大型企业人力资源部为研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了180名员工进行调查,所得数据如下表所示: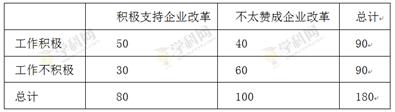
对于人力资源部的研究项目,根据上述数据盘算能否在犯错误的概率不超过0.5%的情况下认为工作积极和支持企业改革有关系.
附:公式及相关数据:
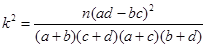 (其中n=a+b+c+d).
(其中n=a+b+c+d).
(本小题满分12分)已知函数 =lnx。
=lnx。
(1)求函数g(x)=f(x)+mx2−4x在定义域内单调递增,求实数m的取值范围;
(2)若b>a>0,求证:f(b)−f(a)> 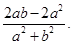
(本小题满分10分)在平面直角坐标系中,曲线C1 的参数方程为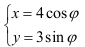 (ϕ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ。
(ϕ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ。
(1)求曲线C2的直角坐标方程;
(2)已知点M是曲线C1上任意一点,点N是曲线C2上任意一点,求|MN|的取值范围。