如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF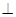 平面EFDC.
平面EFDC.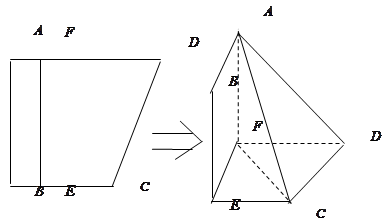
(Ⅰ) 当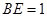 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点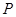 ,且
,且 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出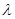 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅱ) 设BE=x,问当x为何值时,三棱锥A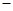 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
(1)求证:平面MOE∥平面PAC;
(2)求证:平面PAC⊥平面PCB;
(3)设二面角M-BP-C的大小为θ,求cosθ的值.
已知函数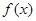 =sin(2x+
=sin(2x+ )+ cos 2x.
)+ cos 2x.
(1)求函数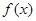 的单调递增区间。
的单调递增区间。
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,已知f(A)= ,a=2,B=
,a=2,B= ,求△ABC的面积.
,求△ABC的面积.
已知数集 ,其中
,其中 ,且
,且 ,若对
,若对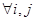 (
(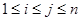 ),
), 与
与 两数中至少有一个属于
两数中至少有一个属于 ,则称数集
,则称数集 具有性质
具有性质
(1)分别判断数集 与数集
与数集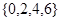 是否具有性质
是否具有性质 ,说明理由
,说明理由
(2)已知数集 具有性质
具有性质 ,判断数列
,判断数列 是否为等差数列,若是等差数列,请证明;若不是,请说明理由
是否为等差数列,若是等差数列,请证明;若不是,请说明理由
设函数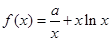 ,
,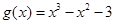
(1)讨论函数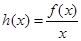 的单调性
的单调性
(2)如果存在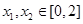 ,使得
,使得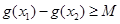 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数
(3)如果对任意的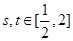 ,都有
,都有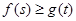 成立,求实数
成立,求实数 的取值范围
的取值范围
已知数列 中
中 ,数列
,数列 中
中 ,其中
,其中
(1)求证:数列 是等差数列
是等差数列
(2)设 是数列
是数列 的前n项和,求
的前n项和,求
(3)设 是数列
是数列 的前n 项和,求证:
的前n 项和,求证: